Advertisements (Quảng cáo)
Cho tam giác ABC vuông tại A. Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại D. Chứng minh rằng:
\({S_{ABC}} = BD.DC\)
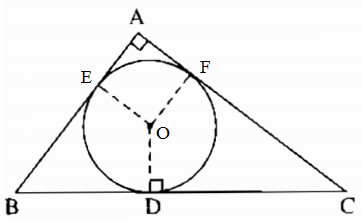
Gọi E và F lần lượt là tiếp điểm của đường
tròn với AB và AC.
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AE = AF
BE = BD
CD = CF
BD = BC + CD
BE = AB – AE
Suy ra: BD + BE = AB + BC – (AE + CD )
= AB + BC – (AE + CE)
= AB + BC – AC
Suy ra: \(BD = {{AB + BC – AC} \over 2}\)
Advertisements (Quảng cáo)
Lại có: CD = BC – BD
CF = AC = AF
Suy ra: CD + CF = BC + AC – ( BD + AF)
= BC + AC – (BE + AE)
= BC + AC – BA
Suy ra: \(CD = {{BC + AC – AB} \over 2}\)
Ta có: \(BD.CD = {{AB + BC – AC} \over 2}.{{BC + AC – AB} \over 2}\)
\(= {{\left[ {BC – (AC – AB)} \right]\left[ {BC + (AC – AB)} \right]} \over 4}\)
\(={{B{C^2} – {{(AC – AB)}^2}} \over 4} = {{B{C^2} – A{C^2} – A{B^2} + 2AB.AC} \over 4}\) (1)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 (2)
Từ (1) và (2) suy ra: \(BD.CD = {{2AB.AC} \over 4} = {{AB.AC} \over 2}\)
Mà \({S_{ABC}} = {1 \over 2}AB.AC\)
Vậy \({S_{ABC}} = BD.DC.\)