Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ các đường kính AOC, AO’D. Chứng minh rằng ba điểm C, B, D thẳng hàng và AB ⊥ CD.. Câu 67 trang 167 Sách bài tập (SBT) Toán 9 Tập 1 - Bài 7. Vị trí tương đối của hai đường tròn
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ các đường kính AOC, AO’D. Chứng minh rằng ba điểm C, B, D thẳng hàng và AB ⊥ CD.

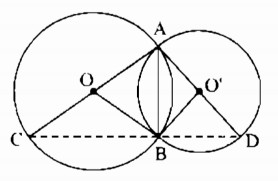
Tam giác ABC nội tiếp trong đường tròn
Advertisements (Quảng cáo)
(O) có AC là đường kính nên \(\widehat {ABC} = 90^\circ \)
Ta có:
\(\widehat {CBD} = \widehat {ABC} + \widehat {ABD} = 90^\circ + 90^\circ = 180^\circ \)
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD.
