Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O).
a) Chứng minh rằng CA, CB là các tiếp tuyến của đường tròn (O’)
b) Đường vuông góc với AO’ tại O’ cắt AB ở I. Đường vuông góc với AC tại C cắt đường thẳng O’B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng.

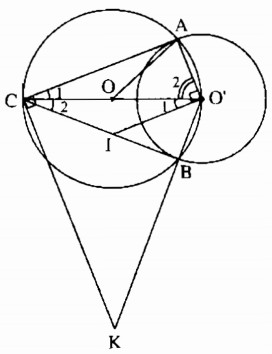
a) Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên \(\widehat {O’AC} = 90^\circ \)
Suy ra: CA ⊥ O’A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O’)
Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên \(\widehat {O’BC} = 90^\circ \)
Suy ra: CB ⊥ O’B tại điểm B
Vậy CB là tiếp tuyến đường tròn (O’)
b) Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C.
Suy ra: \(\widehat {ACO’} = \widehat {BCO’}\) (tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Advertisements (Quảng cáo)
Suy ra: O’I // CA \( \Rightarrow \widehat {ACO’} = \widehat {CO’I}\) (hai góc so le trong)
Suy ra: \(\widehat {BCO’} = \widehat {CO’I}\)
Hay tam giác CIO’ cân tại I ⇒ IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: \(\widehat {AO’C} = \widehat {BO’C}\) (tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A \(\Rightarrow \widehat {AO’C} = \widehat {O’CK}\) (hai góc so le trong)
Suy ra: \(\widehat {O’CK} = \widehat {KO’C}\)
Hay tam giác CKO’ cân tại K ⇒ KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C.
Vậy O, I, K thẳng hàng.
