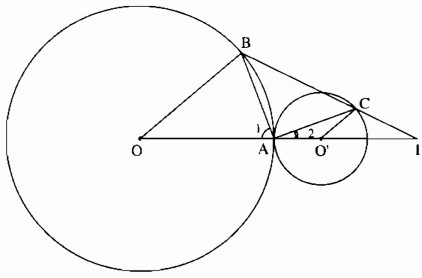
Cho đường tròn (O; 3cm) và đường tròn (O’; 1cm) tiếp xúc ngoài tại A. Vẽ hai bán kính OB và O’C song song với nhau thuộc cùng nửa mặt phẳng có bờ OO’.
a) Tính số đo góc BAC.
b) Gọi I là giao điểm của BC và OO’. Tính độ dài OI.

a) Ta có: OB // O’C (gt)
Suy ra: \(\widehat {AOB} + \widehat {AO’C} = 180^\circ \) (hai góc trong cùng phía)
OA = OB ( = R)
⇒ Tam giác AOB cân tại O.
Suy ra: \(\widehat {BAO} = {{180^\circ - \widehat {AOB}} \over 2}\)
O’A = O’C ( = R)
⇒ Tam giác AO’C cân tại O’
Advertisements (Quảng cáo)
Suy ra: \(\widehat {CAO’} = {{180^\circ - \widehat {AO’C}} \over 2}\)
Ta có: \(\widehat {BAO} + \widehat {CAO’} = {{180^\circ - \widehat {AOB}} \over 2} + {{180^\circ - \widehat {AO’C}} \over 2}\)
\( = {{180^\circ + 180^\circ - (\widehat {AOB} + \widehat {AO’C})} \over 2} = {{180^\circ + 180^\circ - 180^\circ } \over 2} = 90^\circ \)
Lại có: \(\widehat {BAO} + \widehat {BAC} + \widehat {CAO’} = 180^\circ \)
Suy ra: \(\widehat {BAC} = 180^\circ - (\widehat {BAO} + \widehat {CAO’})\)
\( = 180^\circ - 90^\circ = 90^\circ \)
Trong tam giác IBO, ta có: OB // O’C
Suy ra: \({{IO’} \over {IO}} = {{O’C} \over {OB}}\) ( hệ quả định lí Ta-lét)
Suy ra: \({{IO’} \over {IO}} = {1 \over 3} \Rightarrow {{IO - IO’} \over {IO}} = {{3 - 1} \over 3} \Rightarrow {{OO’} \over {IO}} = {2 \over 3}\)
Mà OO’ = OA + O’A = 3 + 1 = 4 (cm)
Suy ra: \({4 \over {IO}} = {2 \over 3} \Rightarrow IO = {{4.3} \over 2} = 6 (cm).\)
