Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, D ∈ (O), E ∈ (O’). Gọi M là giao điểm của BD và CE.
a) Tính số đo góc DAE.
b) Tứ giác ADME là hình gì? Vì sao?
c) Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn.

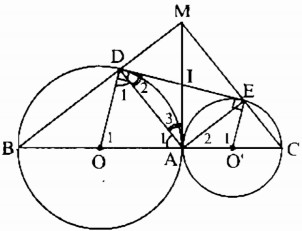
a) Kẻ tiếp tuyến chung tại A cắt DE tại I
Trong đường tròn (O) ta có:
IA = ID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có:
IA = IE (tính chất hai tiếp tuyến cắt nhau)
Advertisements (Quảng cáo)
Suy ra: \(IA = ID = IE = {1 \over 2} DE\)
Tam giác ADE có đường trung tuyến AI ứng với cạnh DE và bằng nửa cạnh DE nên tam giác ADE vuông tại A.
Suy ra: \(\widehat {EAD} = 90^\circ \)
b) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên \(\widehat {ADB} = 90^\circ \) hay \(\widehat {AEM} = 90^\circ \)
Mặt khác: \(\widehat {EAD} = 90^\circ \) (chứng minh trên)
Tứ giác ADME có ba góc vuông nên nó là hình chữ nhật.
c) Tứ giác ADME là hình chữ nhật và ID = IE (chứng minh trên) nên đường chéo
AM của hình chữ nhật phải đi qua trung điểm I của DE. Suy ra: A, I, M thẳng hàng.
Ta có: IA ⊥ OO’ ( vì IA là tiếp tuyến của (O))
Suy ra: AM ⊥ OO’
Vậy MA là tiếp tuyến chung của đường tròn (O) và (O’).
