Tính diện tích phần gạch sọc trên hình sau (theo kích thước đã cho trên hình)
Giải
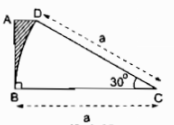
Diện tích phần gạch sọc là hiệu giữa diện tích hình thang ABCD và diện tích hình quạt tròn có góc ở tâm 300 của đường tròn bán kính bằng a.
Từ D kẻ \(DH \bot BC\)
Trong tam giác vuông HDC có \(\widehat {DHC} = {90^0}\)
\(DH = DC.\sin C = a.\sin {30^0} = {a \over 2}\)
\(CH = DC.cos\widehat C = a.cos{30^0} = {{a\sqrt 3 } \over 2}\)
\(BH = BC - HC = a - {{a\sqrt 3 } \over 2} = {{a\left( {2 - \sqrt 3 } \right)} \over 2}\)
Advertisements (Quảng cáo)
\( \Rightarrow AD = {{a\left( {2 - \sqrt 3 } \right)} \over 2}\)
Diện tích của hình thang ABCD bằng:
\({{AD + BC} \over 2}.DH = {{{{a\left( {2 - \sqrt 3 } \right)} \over 2} + a} \over 2}.{a \over 2}\)
\( = {{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8}\)
Diện tích hình quạt tròn bằng: \({{\pi .{a^2}.30} \over {360}} = {{\pi {a^2}} \over {12}}\)
Diện tích phần gạch sọc:
\(S = {{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8} - {{\pi a} \over {12}}\)
\( = {{3{a^2}\left( {4 - \sqrt 3 } \right) - 2\pi {a^2}} \over {24}}\)
\( = {{{a^2}} \over {24}}\left( {12 - 3\sqrt 3 - 2\pi } \right)\)
