Cho nửa đường tròn đường kính AB. Gọi C là một điểm chạy trên nửa đường tròn đó. Trên AC lấy điểm D sao cho AD = CD. Qua A kẻ tiếp tuyến với nửa đường tròn rồi lấy AE = AB (E và C cùng thuộc một nửa mặt phẳng bờ AB)
a) Tìm quỹ tích điểm D
b) Tính diện tích phần chung của hai nửa hình tròn đường kính AB và AE.
Giải
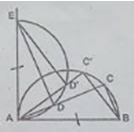
a) Chứng minh thuận
Nối DE. Xét ∆ABC và ∆AED:
AB = AE (gt)
AD = BC (gt)
\(\widehat {EAD} = \widehat {ABC}\) (hệ quả góc giữa tia tiếp tuyến và dây cung)
Suy ra: ∆ABC = ∆EAD (c.g.c) \( \Rightarrow \widehat {EAD} = \widehat {ACB}\)
Mà \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \widehat {EDA} = {90^0}\)
Điểm C chuyển động trên nửa đường tròn đường kính AB thì điểm D luôn nhìn đoạn AE cố định dưới một góc bằng 900, nên điểm D nằm trên nửa đường tròn đường kính AE nằm trong nửa mặt phẳng bờ AE chứa nửa đường tròn đường kính AB.
Chứng minh đảo:
Trên nửa đường tròn đường kính AE lấy điểm D’ bất kỳ, đường thẳng AD’ cắt nửa đường tròn đường kính AB tại C’. Nối ED’, BC’.
Xét ∆AD’E và ∆BC’A:
\(\widehat {D’} = \widehat {C’} = {90^0}\) (các góc nội tiếp chắn nửa đường tròn)
Advertisements (Quảng cáo)
AE = AB (gt)
\(\widehat {EAD} = \widehat {ABC’}\) (2 góc cùng phụ \(\widehat {C’AB}\))
Suy ra: ∆AD’E = ∆BC’A (cạnh huyền, góc nhọn)
\( \Rightarrow AD’ = BC’\)
Vậy khi điểm C chạy trên nửa đường tròn đường kính AB thì quỹ tích điểm D là nửa đường tròn đường kính AE.
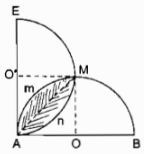
b) Gọi tâm hai nửa đường tròn đường kính AB và AE lần lượt là O và O’, giao điểm thứ hai của hai đường tròn là M
Ta có: OA = OM = O’A = O’M (vì AB = AE)
\(\widehat A = {90^0}\)
Vậy tứ giác AOMO’ là hình vuông
Diện tích phần chung của hai nửa hình tròn bằng diện tích hai quạt tròn có cung \(\overparen{AmM}\) trừ đi diện tích hình vuông
Diện tích hình quạt tròn AOM bằng:
\({{\pi {{\left( {{{AB} \over 2}} \right)}^2}.90} \over {360}} = {{\pi A{B^2}} \over {16}}\)
Diện tích của hình vuông AOMO’ bằng:
\({\left( {{{AB} \over 2}} \right)^2} = {{A{B^2}} \over 4}\)
Diện tích phần chung bằng:
\(2.{{\pi A{B^2}} \over {16}} - {{A{B^2}} \over 4} = {{\pi A{B^2}} \over 8} - {{2A{B^2}} \over 8}\)
\( = {{A{B^2}} \over 8}\left( {\pi - 2} \right)\) (đơn vị diện tích)
