Cho tam giác AHB có \(\widehat H = 90^\circ ,\widehat A = 30^\circ \) và BH = 4cm. Tia phân giác của góc B cắt AH tại O. Vẽ đường tròn (O; OH) và đường tròn (O; OA).
a) Chứng minh đường tròn (O; OH) tiếp xúc với cạnh AB.
b) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.
Giải
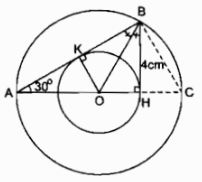
a) Kẻ \(OK \bot AB\)
BO là đường phân giác của \(\widehat B\)
\( \Rightarrow OK = OH\) (tính chất đường phân giác)
Vậy đường tròn (O; OH) tiếp xúc với AB tại K.
b) ∆AHB có \(\widehat H = {90^0}\); \(\widehat A = {30^0}\)
Advertisements (Quảng cáo)
Suy ra: \(\widehat B = {60^0} \Rightarrow \widehat {ABO} = {1 \over 2}\widehat B = {30^0}\)
Suy ra: ∆OAB cân tại O nên OB = OA
Vậy B (O; OA)
∆BHO có \(\widehat H = {90^0}\); \(\widehat {OBH} = {30^0}\)
\(OH = BH.\tan {30^0} = 4.{{\sqrt 3 } \over 3} = {{4\sqrt 3 } \over 3}\) (cm)
\(OB = {{BH} \over {\cos \widehat {OBH}}} = {4 \over {\cos {{30}^0}}} = {4 \over {{{\sqrt 3 } \over 2}}} = {{8\sqrt 3 } \over 3}\) (cm)
Diện tích đường tròn nhỏ: S1 = \(\pi {\left( {{{4\sqrt 3 } \over 3}} \right)^2} = {{16\pi } \over 3}\) (cm2)
Diện tích đường tròn lớn: \({S_2} = \pi {\left( {{{8\sqrt 3 } \over 3}} \right)^2} = {{64\pi } \over 3}\) (cm2)
Diện tích hình vành khăn:
S = \({S_2} - {S_1} = {{64\pi } \over 3} - {{16\pi } \over 3} = {{48\pi } \over 3} = 16\pi \) (cm2)
