Tam giác ABC có . Câu I.1 Trang 123 Sách Bài Tập (SBT) Toán 9 Tập 1 - Ôn tập chương I
Tam giác ABC có \(\widehat A = 105^\circ \), \(\widehat B = 45^\circ \), BC = 4cm. Tính độ dài các cạnh AB, AC.
Gợi ý làm bài
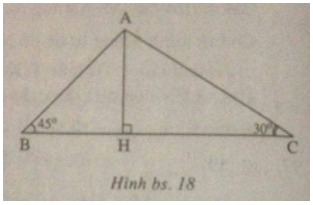
Vẽ đường cao AH. Đặt BH = x, CH = y thì do H nằm giữa B và C ( hai góc $$\widehat B,\widehat C$$ là góc nhọn) suy ra x + y = 4 (xem h.bs.18).
Advertisements (Quảng cáo)
Ta có BH = AH = HCtg30º nên x = \(ytg30^\circ = {y \over {\sqrt 3 }}\).
Vậy ta được \(x + \sqrt {3x} = 4\), suy ra \(x = {4 \over {1 + \sqrt 3 }} \approx 1,46\,(cm)\)
Vậy \(AB = {{AH} \over {\sin 45^\circ }} = {{2AH} \over {\sqrt 2 }} \approx 2,06\,(cm)\)
\(AC = 2AH \approx 1,46.2 = 2,92\,(cm)\)
