Giải mục 1 trang 60, 61, 62 Toán 9 Chân trời sáng tạo tập 1: Có nhận xét gì về hai tam giác OAB và OA’B’?...

Hoạt động1

Trả lời câu hỏi Hoạt động 1 trang 60

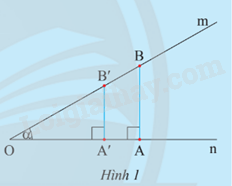
Cho góc nhọn \(\widehat {mOn} = \alpha \). Lấy hai điểm A và A’ trên On, kẻ hai đường thẳng qua A và A’ vuông góc với On và cắt Om lần lượt tại B và B’.

a) Có nhận xét gì về hai tam giác OAB và OA’B’?

b) So sánh các cặp tỉ số?

\(\frac{{AB}}{{OA}}\) và \(\frac{{A’B’}}{{OA’}}\); \(\frac{{AB}}{{OB}}\) và \(\frac{{A’B’}}{{OB’}}\); \(\frac{{OA}}{{OB}}\) và \(\frac{{OA’}}{{OB’}}\).

- Dựa vào định lí: Nếu một góc nhọn của tam giác vuông này bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

- Hai tam giác đồng dạng với nhau thì các cạnh tỉ lệ với nhau.

a) Hai tam giác vuông OAB và OA’B’ đồng dạng với nhau vì:

\(\widehat {A’OB’} = \widehat {AOB}\)

b) Vì \(\Delta OAB\backsim \Delta OA’B’\) nên ta có:

\(\frac{{AB}}{{OA}}\) = \(\frac{{A’B’}}{{OA’}}\); \(\frac{{AB}}{{OB}}\) = \(\frac{{A’B’}}{{OB’}}\); \(\frac{{OA}}{{OB}}\) = \(\frac{{OA’}}{{OB’}}\).

Thực hành1

Trả lời câu hỏi Thực hành 1 trang 61

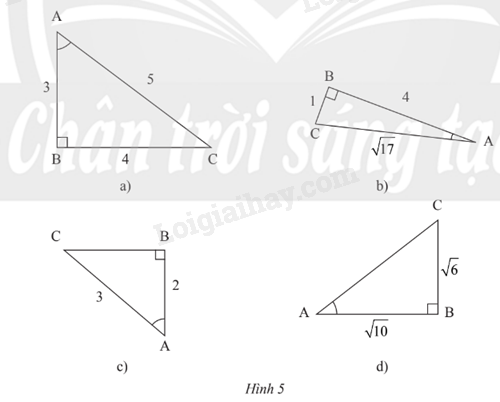
Tính các tỉ số lượng giác của góc nhọn A trong mỗi tam giác vuông ABC có \(\widehat B = {90^o}\) ở Hình 5 (kết quả làm tròn đến hàng phần trăm).

- Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \) . Xét tam giác ABC vuông tại A có \(\widehat {ABC} = \alpha \) , ta có:

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \) .

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \) .

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \) .

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \) .

- Áp dụng định lý Pythagore vào tam giác vuông.

Hình 5a:

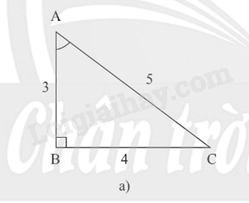
Xét tam giác ABC, \(\widehat B = {90^o}\) ; \(\widehat A = \alpha \) .

Ta có:

sin\(\alpha \) = \(\frac{{BC}}{{AC}} = \frac{4}{5} = 0,8\)

cos \(\alpha \) = \(\frac{{BA}}{{AC}} = \frac{3}{5} = 0,6\)

tan \(\alpha \) = \(\frac{{BC}}{{BA}} = \frac{4}{3} = 1,33\)

cot \(\alpha \) = \(\frac{{BA}}{{BC}} = \frac{3}{4} = 0,75\)

Hình 5b:

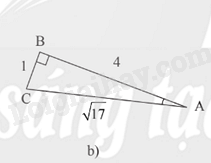
Xét tam giác ABC, \(\widehat B = {90^o}\) ; \(\widehat A = \alpha \) .

Ta có:

sin\(\alpha \) = \(\frac{{BC}}{{AC}} = \frac{1}{{\sqrt {17} }} = 0,24\)

cos \(\alpha \) = \(\frac{{BA}}{{AC}} = \frac{4}{{\sqrt {17} }} = 0,97\)

tan \(\alpha \) = \(\frac{{BC}}{{BA}} = \frac{1}{4} = 0,25\)

cot \(\alpha \) = \(\frac{{BA}}{{BC}} = \frac{4}{1} = 4\)

Hình 5c:

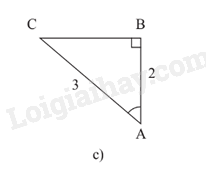
Xét tam giác ABC, \(\widehat B = {90^o}\) ; \(\widehat A = \alpha \) .

Ta có:

BC = \(\sqrt {A{C^2} - A{B^2}} = \sqrt {{3^2} - {2^2}} = \sqrt 5 \)

sin\(\alpha \) = \(\frac{{BC}}{{AC}} = \frac{{\sqrt 5 }}{3} = 0,75\)

cos \(\alpha \) = \(\frac{{BA}}{{AC}} = \frac{2}{3} = 0,67\)

tan \(\alpha \) = \(\frac{{BC}}{{BA}} = \frac{{\sqrt 5 }}{2} = 1,12\)

cot \(\alpha \) = \(\frac{{BA}}{{BC}} = \frac{2}{{\sqrt 5 }} = 0,89\)

Hình 5d:

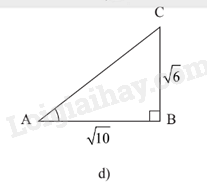
Xét tam giác ABC, \(\widehat B = {90^o}\) ; \(\widehat A = \alpha \) .

Ta có:

AC = \(\sqrt {B{C^2} + A{B^2}} = \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {{\left( {\sqrt {10} } \right)}^2}} = 4\)

sin\(\alpha \) = \(\frac{{BC}}{{AC}} = \frac{{\sqrt 6 }}{4} = 0,612\)

cos \(\alpha \) = \(\frac{{BA}}{{AC}} = \frac{{\sqrt {10} }}{4} = 0,791\)

tan \(\alpha \) = \(\frac{{BC}}{{BA}} = \frac{{\sqrt 6 }}{{\sqrt {10} }} = 0,775\)

cot \(\alpha \) = \(\frac{{BA}}{{BC}} = \frac{{\sqrt {10} }}{{\sqrt 6 }} = 1,291\)

Vận dụng1

Trả lời câu hỏi Vận dụng 1 trang 61

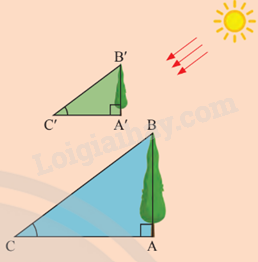
Sử dụng tỉ số lượng giác để giải thích tình huống trong Hoạt động khởi động (Trang 60).

Tại một thời điểm, khi những tia nắng chiếu, cây và bóng tạo thành các tam giác vuông như hình bên. Với \(\widehat C = \widehat {C’}\) , so sánh các tỉ số \(\frac{{AB}}{{AC}}\) và \(\frac{{A’B’}}{{A’C’}}\) .

Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \) . Xét tam giác ABC vuông tại A có \(\widehat {ABC} = \alpha \) , ta có:

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \) .

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \) .

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \) .

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \) .

Với \(\widehat C = \widehat {C’}\) ta có:

tan \(\widehat C\) = tan \(\widehat {C’}\)

Suy ra \(\frac{{AB}}{{AC}} = \frac{{A’B’}}{{A’C’}}\) .

Hoạt động2

Trả lời câu hỏi Hoạt động 2 trang 62

a) Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a (Hình 6a). Tính độ dài cạnh huyền BC theo a, rồi tính các tỉ số lượng giác của góc 45^o .

b) Cho tam giác đều MNP có cạnh bằng a (Hình 6b). Tính độ dài đường cao MH theo a, rồi tính các tỉ số lượng giác của góc 30^o và góc 60^o .

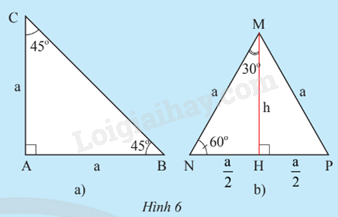
- Áp dụng định lý Pythagore vào tam giác vuông ABC để tính BC, tam giác vuông MHN để tính MH.

- Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \). Xét tam giác ABC vuông tại A có \(\widehat {ABC} = \alpha \) , ta có:

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).

a) Xét tam giác vuông cân ABC:

Áp dụng định lý Pythagore ta có:

BC = \(\sqrt {{a^2} + {a^2}} = a\sqrt 2 \).

Các tỉ số lượng giác của góc 45^o là:

sin 45^o = \(\frac{{AC}}{{BC}} = \frac{a}{{\sqrt 2 a}} = \frac{1}{{\sqrt 2 }}\)

cos 45^o = \(\frac{{AB}}{{BC}} = \frac{a}{{\sqrt 2 a}} = \frac{1}{{\sqrt 2 }}\)

tan 45^o = \(\frac{{AC}}{{AB}} = \frac{a}{a} = 1\)

cot 45^o = \(\frac{1}{{\tan {{45}^o}}} = \frac{1}{1} = 1\)

b) Xét tam giác vuông MHN vuông tại H:

Áp dụng định lý Pythagore ta có:

MH = \(\sqrt {M{N^2} - M{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\).

Các tỉ số lượng giác của góc 30^o là:

sin 30^o = \(\frac{{NH}}{{NM}} = \frac{{\frac{a}{2}}}{a} = \frac{1}{2}\)

cos 30^o = \(\frac{{MH}}{{NM}} = \frac{{\frac{{\sqrt 3 a}}{2}}}{a} = \frac{{\sqrt 3 }}{2}\)

tan 30^o = \(\frac{{NH}}{{MH}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}\)

cot 30^o = \(\frac{1}{{\tan {{30}^o}}} = 1:\frac{{\sqrt 3 }}{3} = \sqrt 3 \)

Các tỉ số lượng giác của góc 60^o là:

sin 30^o = \(\frac{{MH}}{{NM}} = \frac{{\frac{{\sqrt 3 a}}{2}}}{a} = \frac{{\sqrt 3 }}{2}\)

cos 30^o = \(\frac{{NH}}{{NM}} = \frac{{\frac{a}{2}}}{a} = \frac{1}{2}\)

tan 30^o = \(\frac{{MH}}{{NH}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = \sqrt 3 \)

cot 30^o = \(\frac{1}{{\tan {{30}^o}}} = 1:\sqrt 3 = \frac{1}{{\sqrt 3 }}\)

Thực hành2

Trả lời câu hỏi Thực hành 2 trang 62

Tính giá trị biểu thức sau:

a) A = \(\frac{{2\cos {{45}^o}}}{{\sqrt 2 }} + \sqrt 3 \tan {30^o}\)

b) B = \(\frac{{2\sin {{60}^o}}}{{\sqrt 3 }} + \cot {45^o}\)

Dựa vào VD2 trang 62 làm tương tự.

a) A = \(\frac{{2\cos {{45}^o}}}{{\sqrt 2 }} + \sqrt 3 \tan {30^o} = \frac{{2.\frac{{\sqrt 2 }}{3}}}{{\sqrt 2 }} + \sqrt 3 .\frac{{\sqrt 3 }}{3} = \frac{5}{3}\)

b) B = \(\frac{{2\sin {{60}^o}}}{{\sqrt 3 }} + \cot {45^o} = \frac{{2.\frac{{\sqrt 3 }}{2}}}{{\sqrt 3 }} + 1 = 2\).

Vận dụng2

Trả lời câu hỏi Vận dụng 2 trang 62

Tính chiều cao của tháp canh trong Hình 7 (kết quả làm tròn đến hàng phần trăm)

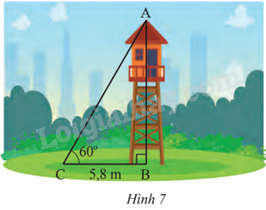
Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \). Xét tam giác ABC vuông tại B có \(\widehat {ACB} = \alpha \) , ta có: tan \(\widehat {ACB} = \frac{{AB}}{{BC}}\). Từ đó suy ra tính chiều cao tháp canh là AB.

Xét tam giác vuông ABC vuông tại B:

Ta có tan\(\widehat {ACB} = \frac{{AB}}{{BC}}\). Suy ra AB = tan\(\widehat {ACB}.BC\) = tan60^o . 5,8 = \(\sqrt 3 .5,8 = 10,046\)

Vậy chiều cao tháp canh là 10,05 m.