Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 8
Cho hàm số \(y = {x^2}\). Ta lập bảng giá trị sau:

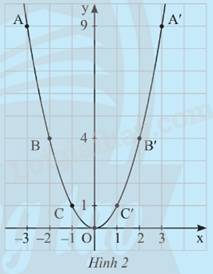
Từ bảng trên, ta lấy các điểm A(-3;9), B(-2;4), C(-1;1), O(0;0), C’(1;1), B’(2;4), A’(3;9) trên mặt phẳng tọa độ Oxy. Đồ thị của hàm số \(y = {x^2}\) là một đường cong đi qua các điểm nêu trên và có dạnh như Hình 2.
Từ đồ thị ở Hình 2, hãy trả lời các câu hỏi sau:
a) Đồ thị của hàm số có vị trí như thế nào so với trục hoành?
b) Có nhận xét gì về vị trí của các cặp điểm A và A’, B và B’, C và C’ so với trục tung?
c) Điểm nào là điểm thấp nhất của đồ thị?

Nhìn vào Hình 2 để nhận xét.

a) Đồ thị của hàm số có vị trí phía trên so với trục hoành.
b) Các cặp điểm A và A’, B và B’, C và C’ đối xứng với nhau qua trục tung.
c) Điểm thấp nhất của đồ thị là điểm O(0;0).
Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 8
Cho hàm số \(y = - \frac{3}{2}{x^2}\).
a) Lập bảng giá trị của hàm số khi x lần lượt nhận các giá trị -2; -1;0;1;2.
b) Vẽ đồ thị của hàm số. Có nhận xét gì về đồ thị của hàm số đó?

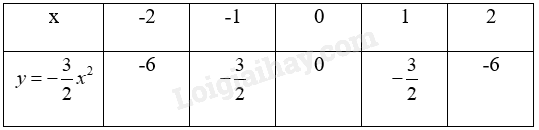
Thay lần lượt giá x vào hàm số \(y = - \frac{3}{2}{x^2}\)để tính y và lập bảng giá trị.
Từ bảng giá trị gọi các điểm và vẽ đồ thị là một đường cong đi qua các điểm trên.

a)
Lấy các điểm A(-2;6), B(-1; \( - \frac{3}{2}\)), O(0;0), B’(1; \( - \frac{3}{2}\)), A’(2;-6).
Đồ thị hàm số \(y = - \frac{3}{2}{x^2}\) là một đường cong đi qua các điểm nêu trên và có dạng như hình dưới.
Advertisements (Quảng cáo)
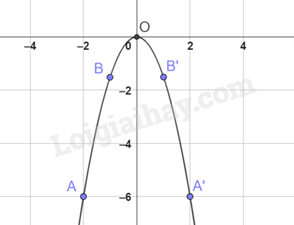
Nhận xét: Đồ thị nằm bên dưới trục hoành.
Thực hành3
Trả lời câu hỏi Thực hành 3 trang 9
Vẽ đồ thị hàm số y = 2x2.

Để vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta thực hiện các bước sau:
+ Lập bảng giá trị của hàm số với một số giá trị của x (thường lấy 5 giá trị gồm số 0 và hai cặp giá trị đối nhau).
+ Trên mặt phẳng tọa độ Oxy, đánh dấu các điểm (x;y) trong bảng giá trị (gồm điểm (0;0) và hai cặp điểm đối xứng nhau qua trục Oy).
+ Vẽ đường parabol đi qua các điểm vừa được đánh dấu.

Bảng giá trị:

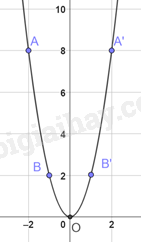
Trên mặt phẳng tọa độ, lấy các điểm A(-2;8), B(-1;2), O(0;0), B’(1;2), A’(2;8)
Đồ thị hàm số y = 2x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.
Vận dụng3
Trả lời câu hỏi Vận dụng 3 trang 10
Động năng (tính bằng J) của một quả bưởi nặng 1 kg rơi với tốc độ v (m/s) được tính bằng công thức \(K = \frac{1}{2}{v^2}\).
a) Tính động năng của quả bưởi đạt được khi nó rơi với tốc độ lần lượt là 3 m/s, 4 m/s.
b) Tính tốc độ rơi của quả bưởi tại thời điểm quả bưởi đạt được động năng 32 J.

Thay v lần lượt bằng 3, 4 vào công thức \(K = \frac{1}{2}{v^2}\) để tính.
Thay K = 32 J để tìm v.

a) Với v = 3 m/s ta có \(K = \frac{1}{2}{.3^2} = \frac{9}{2}\) J
Với v = 4 m/s ta có \(K = \frac{1}{2}{.4^2} = 8\)J
b) Với K = 32 J ta có: \(32 = \frac{1}{2}{v^2}\)
suy ra v2 = 64. Do đó, v = 8 (m/s).
