
Tính các góc của hình thoi có hai đường chéo dài \(2\sqrt 3 \)và 2.

Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường, đường chéo là phân giác của góc hình thoi, hai đường chéo vuông góc với nhau, từ đó ta có tam giác vuông và các số đo các cạnh của tam giác đó, để tính tỉ số lượng giác, giải các góc của hình thoi
Chú ý: Các góc đối của hình thoi bằng nhau.

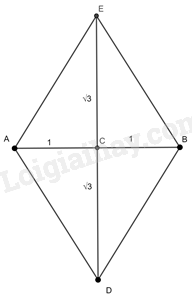
Xét hình thoi ACBE có hai đường chéo ED và đường chéo AB lần lượt là \(2\sqrt 3 \) và 2.
Advertisements (Quảng cáo)
Hai đường chéo cắt nhau tại C nên C là trung điểm của hai đường chéo
Do đó: \(CE = CD = \sqrt 3 ;AC = CB = 1\)
Tam giác ACD vuông tại C (tính chất hai đường chéo của hình thoi) ta có:
\(\tan \widehat {DAC} = \frac{{CD}}{{AC}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \) hay \(\widehat {DAC} = {60^0}\) nên \(\widehat {DAE} = 2\widehat {DAC} = {2.60^0} = {120^0}\) (tính chất hình thoi)
\(\widehat {DAC} + \widehat {ADC} = {90^0}\) (Do tam giác ACD vuông tại C)
Nên \(\widehat {ADC} = {90^0} - {60^0} = {30^0}\) nên \(\widehat {ADB} = 2.\widehat {ADC} = {2.30^0} = {60^0}\)
Vậy hình thoi có các góc là \({120^0}\) và \({60^0}\)
