
Cho hình thang ABCD (AD // BC) có \(AD = 16cm,BC = 4cm,\widehat A = \widehat B = \widehat {ACD} = {90^0}.\)
a) Kẻ đường cao CE của tam giác ACD. Chứng minh \(\widehat {ADC} = \widehat {ACE}.\) Tính sin của các góc \(\widehat {ADC},\widehat {ACE}\) và suy ra \(A{C^2} = AE.AD.\) Từ đó tính AC.
b) Tính góc D của hình thang.

Từ hai góc bằng nhau nên ta có tỉ số lượng giác của hai góc gần như nhau. Từ đó ta lập được tỉ lệ của hai góc này. Rồi tính AC, góc D

Advertisements (Quảng cáo)
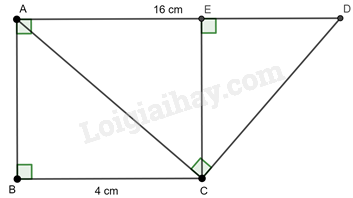
a) Ta có \(\widehat {ADC} = \widehat {ACE}\) (cùng phụ với góc DCE)
Ta có \(\sin \widehat {ADC} = \frac{{AC}}{{AD}};\sin \widehat {ACE} = \frac{{AE}}{{AC}}.\) Từ đó ta có \(\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\) hay \(A{C^2} = AE.AD.\)
AECB là hình chữ nhật do \(\widehat {BAE} = \widehat {ABC} = \widehat {AEC} = {90^0}\) do đó ta có \(AE = BC = 4\) cm.
Nên \(A{C^2} = AE.AD = 4.16 = 64\) hay \(AC = \sqrt {64} = 8\) cm (vì \(AC > 0\))
b) \(\sin \widehat {ADC} = \frac{{AC}}{{AD}}\) hay \(\sin \widehat {ADC} = \frac{8}{{16}} = \frac{1}{2}\) hay \(\sin \widehat {ADC} = {30^0}\)
