
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).
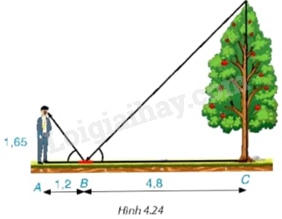

Góc tạo bởi đoạn thẳng nối từ mắt người đứng tới gương và đoạn thẳng AB bằng góc tạo bởi đoạn thẳng nối từ ngọn cây đến gương và đoạn thẳng BC.
Từ đó ta có thể sử dụng tam giác đồng dạng theo trường hợp góc góc để suy ra tỉ lệ các cạnh tương ứng, từ đó ta giải ra được chiều cao của cây, hoặc sử dụng tỉ số lượng giác của hai góc trên (\(\tan \alpha \) ) để tính chiều cao của cây.

Advertisements (Quảng cáo)
Gọi D là điểm tại mắt của người đứng, E là điểm trên đầu ngọn cây, ta có hình vẽ sau;
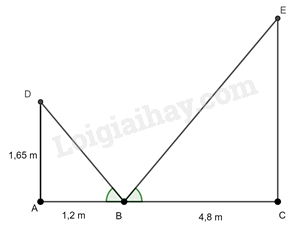
Chiều cao của cây là đoạn EC
Ta có \(\tan \widehat {ABD} = \frac{{1,65}}{{1,2}} = \frac{{11}}{8}\) hay \(\tan \widehat {EBC} = \frac{{11}}{8}\) (do \(\widehat {ABC} = \widehat {DBC}\))
Mà \(\tan \widehat {EBC} = \frac{{EC}}{{BC}}\) suy ra \(\frac{{EC}}{{4,8}} = \frac{{11}}{8}\) hay \(EC = \frac{{11}}{8}.4,8 = 6,6\) m
Vậy chiều cao của cây là 6,6 m.
