
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.

Áp dụng tính chất của hai tiếp tuyến cắt nhau.

a)
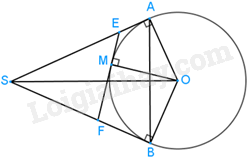
Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA
Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB
Advertisements (Quảng cáo)
\(\begin{array}{*{20}{l}}{{C_{\Delta SEF}} = SE + SF + EF}\\{\; = SE + SF + EM + MF}\\{\; = SE + EA + SF + BF}\\{\; = SA + SB}\end{array}\)
b)
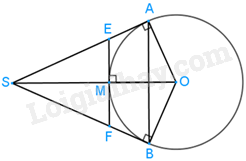
SA và SB là hai tiếp tuyến cắt nhau tại S nên SO là phân giác của góc \(\widehat {{\rm{ASB}}}\).
\( \Rightarrow \widehat {{\rm{OSA}}} = \widehat {{\rm{OSB}}}\) hay \(\widehat {{\rm{MSE}}} = \widehat {{\rm{MSF}}}\)
Xét tam giác SME và tam giác SMF có:
\(\widehat {{\rm{SME}}} = \widehat {{\rm{SMF}}} = 90^\circ \)
SM chung
\(\widehat {{\rm{MSE}}} = \widehat {{\rm{MSF}}}\)
\( \Rightarrow \Delta {\rm{SME}} = \Delta {\rm{SMF}}\) (g.c.g)
\( \Rightarrow {\rm{SE}} = {\rm{SF}}\) (hai cạnh tương ứng)
