Dựa vào tính chất của tam giác cân và hai góc đối đỉnh suy ra \(\widehat {{\rm{OBA}}} = \widehat {{\rm{O’CA}}}\) Khi đó OB // O’C. Phân tích và giải bài tập 5.27 trang 107 SGK Toán 9 tập 1 - Kết nối tri thức Bài 17. Vị trí tương đối của hai đường tròn. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng minh rằng OB // O’C...

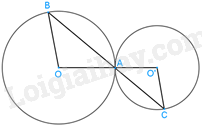
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng minh rằng OB // O’C.

Dựa vào tính chất của tam giác cân và hai góc đối đỉnh suy ra \(\widehat {{\rm{OBA}}} = \widehat {{\rm{O’CA}}}\)
Khi đó OB // O’C.

Advertisements (Quảng cáo)
Vì OA = OB nên tam giác OAB cân tại O.
Suy ra: \(\widehat {{\rm{OBA}}} = \widehat {{\rm{OAB}}}\)
Vì O’A = O’C nên tam giác O’AC cân tại O.
Suy ra: \(\widehat {{\rm{O’AC}}} = \widehat {{\rm{O’CA}}}\)
Lại có: \(\widehat {{\rm{OAB}}} = \widehat {{\rm{O’AB}}}\)
Suy ra: \(\widehat {{\rm{OBA}}} = \widehat {{\rm{O’CA}}}\)
Vậy OB // O’C.
