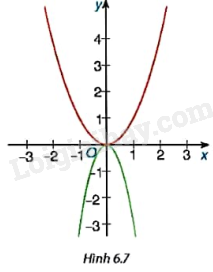
Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong có tính chất. Hướng dẫn cách giải/trả lời bài tập 6.6 trang 9 SGK Toán 9 tập 2 - Kết nối tri thức - Bài 18. Hàm số y = ax^2 (a khác 0). Trong Hình 6.7 có hai đường cong là đồ thị của hai hàm số \(y = - 3{x^2}\) và \(y = {x^2}\). Hãy cho biết đường nào là đồ thị của hàm số \(y = - 3{x^2}\)...

Trong Hình 6.7 có hai đường cong là đồ thị của hai hàm số \(y = - 3{x^2}\) và \(y = {x^2}\). Hãy cho biết đường nào là đồ thị của hàm số \(y = - 3{x^2}\).

Advertisements (Quảng cáo)
Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong có tính chất: Nằm phía trên trục hoành nếu \(a > 0\) và nằm phía dưới trục hoành nếu \(a < 0\).

Vì \({x^2} \ge 0\) với mọi x nên \( - 3{x^2} \le 0\) với mọi x. Do đó, đồ thị hàm số \(y = - 3{x^2}\) gồm các điểm nằm phía dưới trục hoành. Do đó, đường cong màu xanh là đồ thị hàm số \(y = - 3{x^2}\).
