Chứng minh \(\widehat A + \widehat D = {180^o}\), \(\widehat A + \widehat C = {180^o}\) nên \(\widehat C = \widehat D\). Giải chi tiết Giải bài tập 9.21 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức - Bài 29. Tứ giác nội tiếp . Cho hình thang ABCD (AB song song với CD) nội tiếp đường tròn (O).
Câu hỏi/bài tập:

Cho hình thang ABCD (AB song song với CD) nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình thang cân.

+ Chứng minh \(\widehat A + \widehat D = {180^o}\), \(\widehat A + \widehat C = {180^o}\) nên \(\widehat C = \widehat D\).
+ ABCD là hình thang và \(\widehat C = \widehat D\) nên ABCD là hình thang cân.
Advertisements (Quảng cáo)

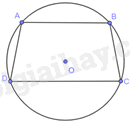
Vì AB//CD nên \(\widehat A + \widehat D = {180^o}\) (hai góc trong cùng phía)
Vì tứ giác ABCD là tứ giác nội tiếp nên \(\widehat A + \widehat C = {180^o}\)
Do đó, \(\widehat C = \widehat D\).
Hình thang ABCD có \(\widehat C = \widehat D\) nên ABCD là hình thang cân.
