Câu hỏi/bài tập:

Người ta muốn dựng một khung cổng hình chữ nhật rộng 4m và cao 3m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa đường tròn như Hình 9.37. Tính chiều dài của đoạn thép làm khung nửa đường tròn đó.
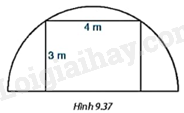

+ Gọi khung cổng hình chữ nhật là ABHG với \(AB = GH = 4m,AG = BH = 3m\). EF là đường kính của nửa đường tròn bao bởi khung cổng.
+ Gọi C là điểm đối xứng với B qua H, D là điểm đối xứng với A qua G.
+ Khi đó, ABCD là hình chữ nhật với \(AB = CD = 4m,AD = BC = 6m\).
+ Hình chữ nhật ABCD nội tiếp đường tròn đường kính AC bằng \(2\sqrt {13} cm\), từ đó tính được chiều dài của đoạn thép làm nửa đường tròn là nửa chu vi của hình tròn đường kính AC.

Advertisements (Quảng cáo)
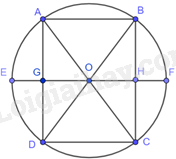
Gọi khung cổng hình chữ nhật là ABHG với \(AB = GH = 4m,AG = BH = 3m\). EF là đường kính của nửa đường tròn bao bởi khung cổng.
Gọi C là điểm đối xứng với B qua H, D là điểm đối xứng với A qua G.
Khi đó, ABCD là hình chữ nhật với \(AB = CD = 4m,AD = BC = 6m\).
Suy ra, hình chữ nhật ABCD nội tiếp đường tròn tâm O, đường kính AC.
Áp dụng định lý Pythagore vào tam giác ABC vuông tại B có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{4^2} + {6^2}} = 2\sqrt {13} \left( m \right)\)
Do đó, chu vi nửa đường tròn đường kính AC là:
\(P = AC.\pi = 2\sqrt {13} \pi \left( {cm} \right)\)
Vậy chiều dài của đoạn khung thép làm nửa đường tròn đó là \(2\sqrt {13} \pi cm\).
