Câu hỏi/bài tập:
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:
- Vẽ đường tròn tâm O bán kính R.
- Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = \frac{{{{360}^o}}}{5} = {72^o}\).
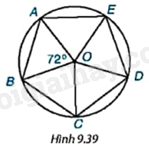
Em hãy giải thích vì sao các cạnh và các góc của đa giác ABCDE bằng nhau (H.9.39).

+ Chứng minh được các tam giác \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\)
Suy ra: \(AE = ED = DC = CB = BA\) và
\(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
+ Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\)
Advertisements (Quảng cáo)

Vì đa giác ABCDE nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE\).
Theo giả thiết: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = {72^o}\)
Do đó, \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\).
Suy ra:
+) \(AE = ED = DC = CB = BA\)
+) \(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
Do đó, \(\widehat {OAE} + \widehat {OAB} = \widehat {OEA} + \widehat {OED} = \widehat {ODE} + \widehat {ODC} = \widehat {OCD} + \widehat {OCB} = \widehat {OBC} + \widehat {OBA}\)
Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\).
Vậy các cạnh và các góc của đa giác ABCDE bằng nhau.
