Câu hỏi/bài tập:

Cho hình thoi ABCD có \(\widehat A = {60^o}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.

+ Chứng minh tam giác ABD đều nên \(BD = AB = AD\).
+ Chứng minh \(MB = BN = PD = DQ = MQ = NP = \frac{{AB}}{2}\).
+ Chứng minh \(\widehat B = \widehat {BNP} = \widehat {NPD} = \widehat D = \widehat {DQM} = \widehat {QMB} = {120^o}\)
+ Suy ra MBNPDQ là lục giác đều.

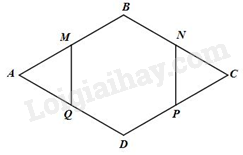
Vì ABCD là hình thoi nên \(AB = BC = CD = AD\).
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên \(MB = BN = NC = PC = PD = DQ = \frac{{AB}}{2}\) (1)
Tam giác ABD có: \(AB = AD\) nên tam giác ABD là tam giác cân tại A, mà \(\widehat A = {60^o}\) nên tam giác ABD đều. Do đó, \(AB = BD\).
Advertisements (Quảng cáo)
Vì M, Q lần lượt là trung điểm của AB và AD (gt) nên MQ là đường trung bình của tam giác ABD. Do đó, \(MQ = \frac{1}{2}BD = \frac{1}{2}AB\) (2).
Vì N, P lần lượt là trung điểm của BC và CD (gt) nên NP là đường trung bình của tam giác CBD. Do đó, \(NP = \frac{1}{2}BD = \frac{1}{2}AB\) (3)
Từ (1), (2) và (3) ta có: \(MB = BN = PD = DQ = MQ = NP\) (*)
Vì ABCD là hình thoi nên \(\widehat {ABC} = \widehat {ADC};\widehat C = \widehat A = {60^o}\)
Ta có:
\(\widehat {ABC} + \widehat {ADC} + \widehat C + \widehat A = {360^o} \Rightarrow \widehat {ABC} = \widehat {ADC} = {360^o} - {2.60^o} = {120^o}\)
Tam giác NPC có: \(NC = PC\) nên tam giác NPC cân tại C. Mà \(\widehat C = {60^o}\) nên tam giác NPC đều.
Do đó, \(\widehat {CNP} = {60^o}\)
Ta có: \(\widehat {BNP} + \widehat {PNC} = {180^o}\) (hai góc kề bù) nên \(\widehat {BNP} = {120^o}\)
Chứng minh tương tự ta có:
\(\widehat {NPD} = \widehat {DQM} = \widehat {QMB} = {120^o}\)
Do đó: \(\widehat {ABC} = \widehat {ADC} = \widehat {BNP} = \widehat {NPD} = \widehat {DQM} = \widehat {QMB} = {120^o}\) (**)
Từ (*) và (**) ta có: MBNPDQ là lục giác đều.
