Câu hỏi/bài tập:

Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.

+ Chứng minh bốn điểm B, F, E, C thuộc đường tròn đường kính BC nên tứ giác BCEF là tứ giác nội tiếp.
+ Chứng minh bốn điểm C, A, F, D thuộc đường tròn đường kính AC nên tứ giác CAFD là tứ giác nội tiếp.
+ Chứng minh bốn điểm B, A, E, D thuộc đường tròn đường kính BA nên tứ giác ABDE là tứ giác nội tiếp.
Advertisements (Quảng cáo)

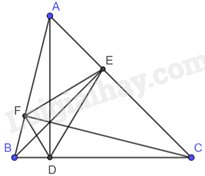
Vì AD, BE, CF là các đường cao của tam giác ABC nên \(AD \bot BC,BE \bot AC,CF \bot AB\).
Do đó, \(\widehat {ADB} = \widehat {ADC} = \widehat {BEC} = \widehat {BEA} = \widehat {AFC} = \widehat {CFB} = {90^o}\).
Vì \(\widehat {BFC} = \widehat {BEC} = {90^o}\) nên tam giác BFC vuông tại F và tam giác BEC vuông tại E. Do đó, hai điểm E, F thuộc đường tròn đường kính BC. Do đó, tứ giác BCEF là tứ giác nội tiếp.
Vì \(\widehat {AFC} = \widehat {ADC} = {90^o}\) nên tam giác AFC vuông tại F và tam giác ADC vuông tại D. Do đó, hai điểm D, F thuộc đường tròn đường kính AC. Do đó, tứ giác CAFD là tứ giác nội tiếp.
Vì \(\widehat {ADB} = \widehat {AEB} = {90^o}\) nên tam giác ADB vuông tại D và tam giác AEB vuông tại E. Do đó, hai điểm E, D thuộc đường tròn đường kính BA. Do đó, tứ giác ABDE là tứ giác nội tiếp.
