Câu hỏi/bài tập:

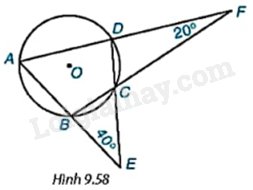
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết \(\widehat {BEC} = {40^o}\) và \(\widehat {DFC} = {20^o}\), tính số đo các góc của tứ giác ABCD.

+ Tính góc BCD, góc ADC, góc ABC theo góc A bằng cách sử dụng tính chất tứ giác nội tiếp và tổng các góc trong một tam giác.
+ Sử dụng kiến thức tổng các góc trong một tứ giác để tính góc A, từ đó tính được các góc còn lại.

Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat A + \widehat {BCD} = {180^o} \Rightarrow \widehat {BCD} = {180^o} - \widehat A\)
Advertisements (Quảng cáo)
Tam giác ADE có:
\(\widehat {ADC} = {180^o} - \widehat E - \widehat A = {140^o} - \widehat A\)
Tam giác ABF có:
\(\widehat {ABC} = {180^o} - \widehat F - \widehat A = {160^o} - \widehat A\)
Tứ giác ABCD có:
\(\widehat A + \widehat {BCD} + \widehat {ABC} + \widehat {ADC} = {360^o}\)
\( \Rightarrow \widehat A + {180^o} - \widehat A + {140^o} - \widehat A + {160^o} - \widehat A = {360^o}\)
\( \Rightarrow {480^o} - 2\widehat A = {360^o} \Rightarrow \widehat A = {60^o}\)
Do đó, \(\widehat {BCD} = {120^o},\widehat {ADC} = {80^o},\widehat {ABC} = {100^o}\)
