Câu hỏi/bài tập:

Cho hình vuông ABCD có cạnh bằng 4cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.

+ Gọi O là giao điểm của hai đường chéo.
+ Chứng minh \(OA = OB = OC = OD\) nên đường tròn ngoại tiếp hình vuông ABCD là đường tròn tâm O, bán kính OD.
+ Áp dụng định lý Pythagore vào tam giác ADB vuông tại A tính DB.
+ Chu vi đường tròn ngoại tiếp hình vuông ABCD là:
\({C_1} = \pi .DB\)
+ Diện tích hình tròn ngoại tiếp hình vuông ABCD là:
\({S_1} = \pi .O{D^2}\)
+ Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.
+ Chứng minh các \(OE = OH = OF = OG\), suy ra, đường tròn (O; OE) nội tiếp hình vuông ABCD.
+ Tính \(OE = AE = \frac{{AB}}{2}\)
+ Chu vi đường tròn nội tiếp hình vuông ABCD là:
\({C_2} = 2\pi .OE\)
+ Diện tích hình tròn nội tiếp hình vuông ABCD là:
\({S_2} = \pi .O{E^2}\)

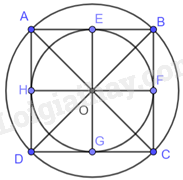
Gọi O là tâm của hình vuông ABCD. Do đó, đường tròn ngoại tiếp hình vuông ABCD là đường tròn tâm O, bán kính OD.
Áp dụng định lý Pythagore vào tam giác ADB vuông tại A có:
Advertisements (Quảng cáo)
\(A{B^2} + A{D^2} = D{B^2} \Rightarrow DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \left( {cm} \right) \Rightarrow OD = 2\sqrt 2 \left( {cm} \right)\)
Chu vi đường tròn ngoại tiếp hình vuông ABCD là:
\({C_1} = \pi .DB = 4\sqrt 2 \pi \left( {cm} \right)\)
Diện tích hình tròn ngoại tiếp hình vuông ABCD là:
\({S_1} = \pi .O{D^2} = \pi .{\left( {2\sqrt 2 } \right)^2} = 8\pi \left( {c{m^2}} \right)\)
Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.
Tam giác AOB có: \(OA = OB\) (bán kính đường tròn (O)) nên tam giác OAB cân tại O. Do đó, OE là đường trung tuyến đồng thời là đường cao.
Do đó, \(OE \bot AB \Rightarrow \widehat {OEA} = \widehat {OEB} = {90^o}\)
Chứng minh tương tự ta có:
\(\widehat {OFB} = \widehat {OFC} = \widehat {OGC} = \widehat {OGD} = \widehat {OHD} = \widehat {OHA} = {90^o}\)
Tứ giác AEOH có: \(\widehat {HAE} = \widehat {OEA} = \widehat {OHA} = {90^o}\) nên tứ giác AEOH là hình chữ nhật.
Mà AO là tia phân giác của góc HAE (do ABCD là hình vuông) nên AEOH là hình vuông.
Do đó, \(OE = OH\).
Chứng minh tương tự ta có:
\(OE = OF,OF = OG,OG = OH\)
Do đó: \(OE = OH = OF = OG\). Suy ra, đường tròn (O; OE) nội tiếp hình vuông ABCD.
Ta có: \(OE = AE = \frac{{AB}}{2} = 2cm\)
Chu vi đường tròn nội tiếp hình vuông ABCD là:
\({C_2} = 2\pi .OE = 2\pi .2 = 4\pi \left( {cm} \right)\)
Diện tích hình tròn nội tiếp hình vuông ABCD là:
\({S_2} = \pi .O{E^2} = \pi {.2^2} = 4\pi \left( {c{m^2}} \right)\)
