Câu hỏi/bài tập:
Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp một đường tròn bán kính 2cm (H.9.40) thì độ dài các cạnh của lục giác đều đó bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?
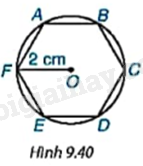

+ Chứng minh \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra
\(\widehat {FOA} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{6} = {60^o}\)
+ Chứng minh tam giác AOB đều, từ đó tính được AB và \(\widehat {OAB} = \widehat {OBA} = {60^o}\).
+ Tính được \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\).

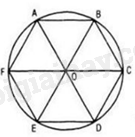
Vì ABCDEF là lục giác đều \(AB = BC = CD = DE = EF = FA\).
Advertisements (Quảng cáo)
Mà lục giác ABCDEF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).
Do đó, \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Do đó,
+) \(\widehat {FOA}\)\( = \widehat {AOB}\)\( = \widehat {BOC}\)\( = \widehat {COD}\)\( = \widehat {DOE}\)\( = \widehat {EOF}\)\( = \frac{{{{360}^o}}}{6}\)\( = {60^o}\)
+) \(\widehat {OAF}\)\( = \widehat {OFA}\)\( = \widehat {OEF}\)\( = \widehat {OFE}\)\( = \widehat {ODE}\)\( = \widehat {OED}\)\( = \widehat {ODC}\)\( = \widehat {OCD}\)\( = \widehat {OCB}\)\( = \widehat {OBC}\)\( = \widehat {OBA}\)\( = \widehat {OAB}\)
Tam giác AOB có: \(OA = OB,\widehat {AOB} = {60^o}\) nên tam giác OAB đều.
Do đó, \(OA = AB = 2cm\) và \(\widehat {OAB} = \widehat {OBA} = {60^o}\)
Suy ra:
\(\widehat {OAF} + \widehat {OAB}\)\( = \widehat {OFA} + \widehat {OFE}\)\( = \widehat {OEF} + \widehat {OED}\)\( = \widehat {ODE} + \widehat {ODC}\)\( = \widehat {OCD} + \widehat {OCB}\)\( = \widehat {OBC} + \widehat {OBA}\)\( = {60^o} + {60^o}\)\( = {120^o}\)
Do đó: \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\)
Vậy lục giác đều ABCDEF nội tiếp (O) bán kính 2cm có độ dài cạnh bằng 2cm và số đo các góc lục giác đều bằng \({120^o}\)
