Câu hỏi/bài tập:
a) Vẽ tam giác đều ABC. Hãy trình bày cách xác định tâm của đường tròn ngoại tiếp tam giác ABC và vẽ đường tròn đó.
b) Giải thích vì sao tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó (H.9.17).
c) Giải thích vì sao \(\widehat {OBM} = {30^o}\) và \(OB = \frac{{\sqrt 3 }}{3}BC\) (với M là trung điểm của BC).
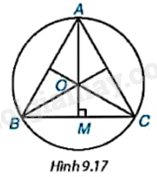

a) Kẻ ba đường trung trực của các cạnh AB, AC, BC. Gọi O là giao điểm của ba đường trung trực đó thì O là tâm của đường tròn ngoại tiếp tam giác ABC.
b) + Trong tam giác đều, giao điểm của ba đường trung trực đồng thời là trọng tâm của tam giác đó.
+ Suy ra, tâm O đường tròn ngoại tiếp trùng với trọng tâm của tam giác đó.
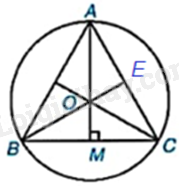
c) Gọi E là giao điểm của BO và AC.
+ Chứng minh BE là đường phân giác và trung tuyến của tam giác đều ABC.
Do đó, \(OB = \frac{2}{3}BE\), \(\widehat {OBM} = {30^o}\)
+ Áp dụng định lý Pythagore vào tam giác BEC để tính BE, từ đó tính OB.
Advertisements (Quảng cáo)

a) Kẻ ba đường trung trực của các cạnh AB, AC, BC. Gọi O là giao điểm của ba đường trung trực đó thì O là tâm của đường tròn ngoại tiếp tam giác ABC.
b) Vì tam giác ABC đều nên O vừa là giao điểm của ba đường trung trực trong tam giác, vừa là trọng tâm của tam giác. Do đó, tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó.
c) Tam giác ABC đều nên \(BC = AC,\widehat {ABC} = {60^o}\)
Gọi E là giao điểm của BO và AC. Khi đó, BE là đường trung trực của tam giác ABC.
Vì tam giác ABC đều nên BE là đường trung trực, đường trung tuyến và đường phân giác của tam giác.
Do đó, \(OB = \frac{2}{3}BE\) và \(\widehat {OBM} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}{.60^o} = {30^o}\).
Vì E là trung điểm của AC nên \(EC = \frac{{AC}}{2} = \frac{{BC}}{2}\).
Tam giác BEC vuông tại E nên theo định lý Pythagore ta có:
\(B{E^2} + E{C^2} = B{C^2}\)
\(BE = \sqrt {B{C^2} - E{C^2}} = \sqrt {B{C^2} - {{\left( {\frac{{BC}}{2}} \right)}^2}} = \frac{{BC\sqrt 3 }}{2}\)
\(OB = \frac{2}{3}.\frac{{BC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3}BC\)
