Câu hỏi
Trả lời câu hỏi Câu hỏi trang 67
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
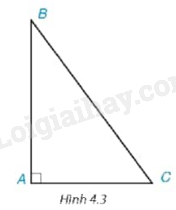

Góc B tạo bởi hai cạnh là AB và BC trong đó cạnh BC là cạnh huyền và cạnh AB là cạnh kề, cạnh còn lại của tam giác là cạnh đối.

Góc C có cạnh đối là AB và cạnh kề của góc C là AC.
Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 67
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B’} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A’B’C’;\)
b) \(\frac{{AC}}{{BC}} = \frac{{A’C’}}{{B’C’}};\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}};\frac{{AC}}{{AB}} = \frac{{A’C’}}{{A’B’}};\frac{{AB}}{{AC}} = \frac{{A’B’}}{{A’C’}}\)

Chứng minh tam giác đồng dạng theo trường hợp góc – góc (tam giác có hai cặp góc tương ứng bằng nhau) , sử dụng tính chất của tỉ lệ thức để chứng minh ý b (\(\frac{a}{b} = \frac{c}{d}\) suy ra \(\frac{a}{c} = \frac{b}{d}\) và \(\frac{b}{a} = \frac{d}{c}\) (tính chất tỉ lệ thức) ) .

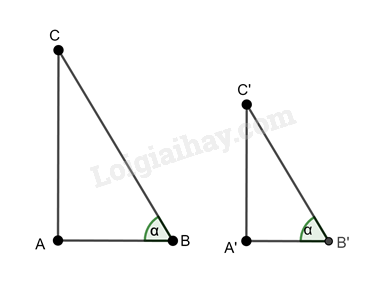
a) Xét hai tam giác ABC và tam giác A’B’C’ ta có:
\(\begin{array}{l}\widehat A = \widehat {A’} = {90^0}\\\widehat B = \widehat {B’} = \alpha \end{array}\)
Nên \(\Delta ABC\backsim \Delta A’B’C’\left( g-g \right)\)
b) \(\Delta ABC\backsim \Delta A’B’C’\) suy ra \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{AC}}{{A’C’}}\) (tỉ lệ các cạnh tương ứng)
Do \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}}\) nên ta có \(\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}}\) (tính chất tỉ lệ thức)
Do \(\frac{{BC}}{{B’C’}} = \frac{{AC}}{{A’C’}}\) nên ta có \(\frac{{A’C’}}{{B’C’}} = \frac{{AC}}{{BC}}\) (tính chất tỉ lệ thức)
Do \(\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}\) nên ta có \(\frac{{AB}}{{AC}} = \frac{{A’B’}}{{A’C’}}\) và \(\frac{{AC}}{{AB}} = \frac{{A’B’}}{{A’C’}}\) (tính chất tỉ lệ thức)
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 68
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.

Xét tam giác ABC vuông tại A, ta có:
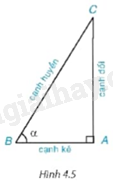
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc B, kí hiệu \(\sin \widehat B\)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc B, kí hiệu \(\cos \widehat B\)
Tỉ số giữa cạnh đối và cạnh kề của góc B gọi là \(\tan \widehat B\)
Tỉ số giữa cạnh kề và cạnh đối của góc B gọi là \(\cot \widehat B\)
Ở bài toán này ta còn thiếu cạnh huyền BC, do đó cần sử dụng định Pythagore để tính.

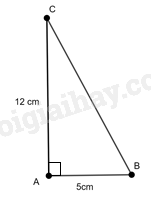
Xét tam giác ABC vuông tại A, ta có \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {5^2} + {12^2} = 169\) suy ra \(BC = 13\) (cm) .
Theo định nghĩa của tỉ số lượng giác ta có:
\(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{12}}{{13}};\\\cos \widehat B = \frac{{AB}}{{BC}} = \frac{5}{{13}};\\\tan \widehat B = \frac{{AC}}{{AB}} = \frac{{12}}{5};\\\cot \widehat B = \frac{{AB}}{{AC}} = \frac{5}{{12}}\)
Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 69
Cho tam giác ABC vuông cân tại A và \(AB = AC = a\) (H.4.7a).
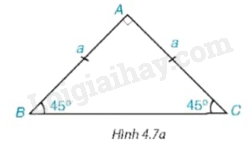
Advertisements (Quảng cáo)
a) Hãy tính BC và các tỉ số \(\frac{{AB}}{{BC}}\) và \(\frac{{AC}}{{BC}}.\) Từ đó suy ra \(\sin {45^0};\cos {45^0}.\)
b) Hãy tính các tỉ số \(\frac{{AB}}{{AC}}\) và \(\frac{{AC}}{{AB}}.\) Từ đó suy ra \(\tan {45^0};\cot {45^0}.\)

Tính BC theo định lý Pythagore ta có: \(B{C^2} = A{B^2} + A{C^2}\)
Để tính các tỉ số ta thay các độ đo tương ứng của các cạnh.

Tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {a^2} + {a^2} = 2{a^2}\) suy ra \(BC = a\sqrt 2 \)
a) Tỉ số \(\frac{{AB}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) và \(\frac{{AC}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\).
Do đó \(\sin {45^0} = \sin \widehat B = \frac{{AC}}{{BC}} = \frac{{\sqrt 2 }}{2};\) \(\cos {45^0} = \cos \widehat B = \frac{{AB}}{{BC}} = \frac{{\sqrt 2 }}{2}.\)
b) Tỉ số \(\frac{{AB}}{{AC}} = \frac{a}{a} = 1;\) \(\frac{{AC}}{{AB}} = \frac{a}{a} = 1\)
Do đó \(\tan {45^0} = \tan \widehat B = \frac{{AC}}{{AB}} = 1;\) \(\cot {45^0} = \cot \widehat B = \frac{{AB}}{{AC}} = 1\)
Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 69
Xét tam giác đều ABC có cạnh bằng 2a.
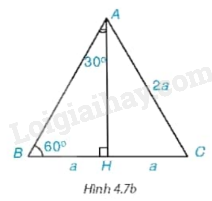
a) Tính đường cao AH của tam giác ABC (H.4.7b) .
b) Tính \(\sin {30^0};\cos {30^0};\sin {60^0};\cos {60^0}.\)
c) Tính \(\tan {30^0};\cot {30^0};\tan {60^0};\cot {60^0}.\)

Chú ý trong tam giác đều, đường cao vừa là đường phân giác vừa là đường trung tuyến. Từ đó ta tính được cạnh AH và các tỉ số lượng giác liên quan.

a) Tam giác ABC đều có đường cao AH nên AH cũng là đường trung tuyến của tam giác. Do đó ta có H là trung điểm của BC nên \(BH = HC = \frac{{BC}}{2} = \frac{{2a}}{2} = a\)
Xét tam giác ABH vuông tại H, ta có: \(A{B^2} = A{H^2} + H{B^2}\) (Đjnh lý Pythagore)
Suy ra \({\left( {2a} \right)^2} = A{H^2} + {a^2}\) nên \(A{H^2} = 3a\) hay \(AH = a\sqrt 3 \)
b) Tam giác ABC đều nên \(\widehat A = \widehat B = \widehat C = {60^0}\)
Nên \(\cos {60^0} = \cos \widehat B = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\sin {60^0} = \sin \widehat B = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác của góc A, do đó \(\widehat {BAH} = \widehat {CAH} = \frac{{\widehat {BAC}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\)
\(\sin {30^0} = \sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\cos {30^0} = \cos \widehat {BAH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
c) \(\tan {30^0} = \tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
\(\cot {30^0} = \cot \widehat {BAH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\tan {60^0} = \tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\cot {60^0} = \tan \widehat {ABH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 70
Cho tam giác ABC vuông tại A có \(\widehat C = {45^0}\) và \(AB = c.\) Tính BC và AC theo c.

Từ công thức lượng giác liên quan đến góc C, ta tính được các cạnh còn lại theo AB.
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc C, kí hiệu \(\sin \widehat C\)
Tỉ số giữa cạnh đối và cạnh kề của góc C gọi là \(\tan \widehat C\)

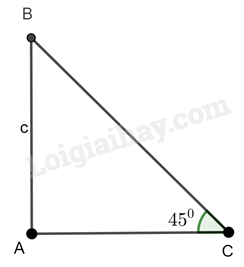
Ta có: \(\tan \widehat C = \frac{{AB}}{{AC}}\) suy ra \(\tan {45^0} = \frac{c}{{AC}}\) do đó \(1 = \frac{c}{{AC}}\) hay \(AC = c\)
\(\sin \widehat C = \frac{{AB}}{{BC}}\) suy ra \(\sin {45^0} = \frac{c}{{BC}}\) do đó \(\frac{{\sqrt 2 }}{2} = \frac{c}{{BC}}\) hay \(BC = \frac{{2c}}{{\sqrt 2 }} = \sqrt 2 c\)
