Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 70
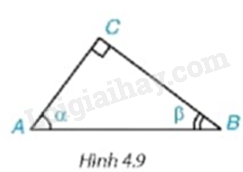
Cho tam giác ABC vuông tại C, có \(\widehat A = \alpha ,\widehat B = \beta \) (H.4.9) . Hãy viết các tỉ số lượng giác của góc \(\alpha ,\beta \) theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.

Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc \(\alpha \), kí hiệu \(\sin \widehat B\)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \widehat B\)
Tỉ số giữa cạnh đối và cạnh kề của góc \(\alpha \) gọi là \(\tan \widehat \alpha \)
Tỉ số giữa cạnh kề và cạnh đối của góc \(\alpha \) gọi là \(\cot \widehat \alpha \)

Ta có:
Advertisements (Quảng cáo)
\(\sin \alpha = \frac{{BC}}{{AB}};\) \(\cos \alpha = \frac{{AC}}{{AB}};\) \(\tan \alpha = \frac{{BC}}{{AC}};\) \(\cot \alpha = \frac{{AC}}{{BC}}\)
\(\sin \beta = \frac{{AC}}{{AB}};\) \(\cos \beta = \frac{{BC}}{{AB}};\) \(\tan \beta = \frac{{AC}}{{BC}};\) \(\cot \beta = \frac{{BC}}{{AC}}\)
Từ đó ta có
\(\sin \alpha = \cos \beta ;\) \(\cos \alpha = \sin \beta ;\) \(\tan \alpha = \cot \beta ;\) \(\cot \alpha = \tan \beta .\)
Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 70
Hãy giải thích tại sao \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)

Nếu hai góc phụ nhau (tổng số đo hai góc bằng \({90^0}\)) thì sin góc này bằng cosin góc kia, tan góc này bằng cot góc kia.

Vì \({35^0} + {55^0} = {90^0}\) nên \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)
