Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 6
Cho hàm số \(y = 2{x^2}\).
a) Hoàn thành bảng giá trị sau vào vở:

b) Trong mặt phẳng Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;2{x^2}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị của hàm số \(y = 2{x^2}\).

a) Thay lần lượt các giá trị \(x = - 3;x = - 2;x = - 1;x = 0;x = 1;x = 2;x = 3\) vào hàm số \(y = 2{x^2}\) ta sẽ tìm được y tương ứng, từ đó hoàn thành được bảng.
b) Cách biểu diễn điểm \(A\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ Oxy:
+ Dựng đường thẳng vuông góc với trục Ox tại \({x_0}\).
+ Dựng đường thẳng vuông góc với trục Oy tại \({y_0}\).
+ Hai đường thẳng vừa dựng trên cắt nhau tại A.
Khi đó, ta đã biểu diễn được điểm \(A\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ Oxy.

a)

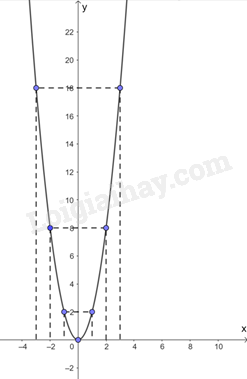
b) Biểu diễn các điểm \(\left( { - 3;18} \right);\left( { - 2;8} \right);\left( { - 1;2} \right);\left( {0;0} \right);\left( {3;18} \right);\left( {2;8} \right);\left( {1;2} \right)\) trên mặt phẳng tọa độ Oxy ta được:
Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 6
Xét đồ thị của hàm số \(y = 2{x^2}\) đã vẽ ở HĐ3 (H.6.3).
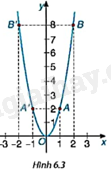
a) Đồ thị nằm về phía trên hay phía dưới trục hoành? Điểm nào là điểm thấp nhất của đồ thị hàm số.
b) So sánh hoành độ và tung độ các cặp điểm thuộc đồ thị: A(1; 2) và \(A’\left( { - 1;2} \right)\); B(2; 8) và \(B’\left( { - 2;8} \right)\).
Từ đó, hãy nhận xét mối liên hệ về vị trí giữa các cặp điểm nêu trên.
c) Tìm điểm C có hoành độ \(x = \frac{1}{2}\) thuộc đồ thị. Xác định tọa độ của điểm C’ đối xứng với điểm C qua trục tung Oy và cho biết điểm C’ có thuộc đồ thị hàm số hay không.

a, b) Dựa vào đọc đồ thị hàm số để đưa ra nhận xét.
c) + Thay \(x = \frac{1}{2}\) vào hàm số \(y = 2{x^2}\) để tìm y.
+ Sử dụng tính chất: Hai điểm (x; y) và \(\left( { - x;y} \right)\) đối xứng nhau qua trục tung Oy.
Từ đó tìm được tọa độ C’.
+ Thay tọa độ của điểm C’ vào hàm số \(y = 2{x^2}\) để chứng minh điểm C’ thuộc đồ thị hàm số.

a) Đồ thị hàm số nằm phía trên trục hoành. Điểm O (0; 0) là điểm thấp nhất của đồ thị.
Advertisements (Quảng cáo)
b) Hai điểm A(1; 2) và \(A’\left( { - 1;2} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
Hai điểm B(2; 8) và \(B’\left( { - 2;8} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
c) Với \(x = \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) thì \(y = 2.{\left( {\frac{1}{2}} \right)^2} = \frac{1}{2}\). Do đó, \(C\left( {\frac{1}{2};\frac{1}{2}} \right)\).
Vì điểm C’ đối xứng với điểm C qua trục Oy nên \(C’\left( { - \frac{1}{2};\frac{1}{2}} \right)\)
Với \(x = - \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) ta có: \(2.{\left( { - \frac{1}{2}} \right)^2} = \frac{1}{2} = {y_{C’}}\)
Do đó, điểm \(C’\left( { - \frac{1}{2};\frac{1}{2}} \right)\) thuộc đồ thị hàm số \(y = 2{x^2}\).
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 8
Vẽ đồ thị của hàm số \(y = \frac{1}{2}{x^2}\). Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.

Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).

Lập bảng một số cặp giá trị tương ứng của x và y:

Biểu diễn các điểm \(\left( { - 4;8} \right),\left( { - 2;2} \right);\left( { - 1;\frac{1}{2}} \right);\left( {0;0} \right);\left( {4;8} \right),\left( {2;2} \right);\left( {1;\frac{1}{2}} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như hình vẽ.
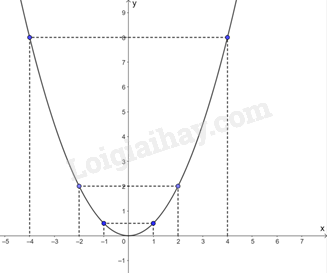
Các điểm thuộc đồ thị hàm số có tung độ bằng 2 là \(\left( { - 2;2} \right)\) và \(\left( {2;2} \right)\). Hai điểm này đối xứng với nhau qua trục Oy.
Vận dụng2
Trả lời câu hỏi Vận dụng 2 trang 8
Giải quyết bài toán ở tình huống mở đầu.
Tình huống mở đầu
Một cây cầu treo có trụ tháp đôi cao 75m so với mặt của cây cầu và cách nhau 400m. Các dây cáp có dạng đồ thị của hàm số \(y = ax^2 (a \ne 0)\) như Hình 6.1 và được treo trên các đỉnh tháp. Tính chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100m (giả sử mặt của cây cầu là bằng phẳng).
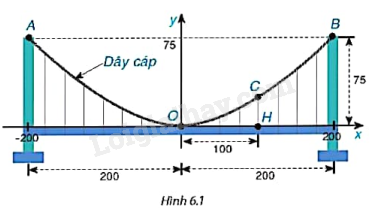

+ Thay điểm (200; 75) vào hàm số \(y = a{x^2}\) ta tìm được a. Viết lại hàm số đã tìm được.
+ Thay \(x = 100\) vào hàm số đã tìm được ta tính được y, giá trị y chính là chiều cao của cây cầu.

Đồ thị hàm số \(y = a{x^2}\) đi qua điểm (200; 75) nên ta có: \(75 = a{.200^2} \Rightarrow a = \frac{3}{{1600}}\).
Khi đó, \(y = \frac{3}{{1600}}{x^2}\).
Với \(x = 100\) ta có: \(y = \frac{3}{{1600}}{.100^2} = \frac{{75}}{4}\).
Vậy chiều cao \(CH = \frac{{75}}{4}m\) khi điểm H cách tâm O của cây cầu 100m.
