Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 75
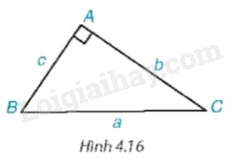
Xét tam giác ABC trong Hình 4.16.
a) Viết các tỉ số lượng giác tang, cotang của góc B và góc C theo b và c.
b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.

Tỉ số giữa cạnh đối và cạnh kề gọi là tan của góc B, kí hiệu \(\tan \widehat B\)
Tỉ số giữa cạnh kề và cạnh đối gọi là cot của góc B, kí hiệu \(\cot \widehat B\)
Và nếu hai góc phụ nhau (tổng số đo hai góc bằng \({90^0}\)) thì sin góc này bằng cosin góc kia, tan góc này bằng cot góc kia.

a) Tam giác ABC vuông tại A, ta có:
\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{b}{c}\)
Advertisements (Quảng cáo)
\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{c}{b}\)
b) Ta có \(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{b}{c}\) nên \(b = c.\tan \widehat B = c.\cot \widehat C\)
Ta có \(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{c}{b}\) nên \(c = b.\cot \widehat B = b.\tan \widehat C\)
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 76
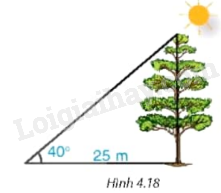
Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm) , biết rằng tia nắng mặt trời tạo với mặt đất góc \({40^0}\) (H.4.18).

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề.

Chiều cao của cây là \(25.\tan {40^0} = 20,98\) m.
Vậy chiều cao của cây khoảng 20,98 m.
