
Cho đường tròn (O) đường kính BC = 2R. Lấy điểm A thuộc đường tròn sao cho AB < AC. Tiếp tuyến tại A cắt tiếp tuyến tại B và C của đường tròn tại E và F.
a) Chứng minh rằng EF = EB + FC.
b) Chứng minh rằng \(BE.CF = {R^2}\).
c) Gọi M là giao điểm của EC và BF. Kẻ đường cao AH của tam giác ABC ( H thuộc BC). Chứng minh rằng ba điểm A, M, H thẳng hàng.
d) Trường hợp cho AB = R, chứng minh rằng tam giác AFC đều, tính theo R diện tích tam giác AFC.
a) Áp dụng tính chất 2 tiếp tuyến cắt nhau.
b) Chứng minh tam giác OEF vuông tại O. Áp dụng hệ thức lượng trong tam giác vuông.
c) Áp dụng định lí Ta-lét đảo chứng mính AM // BE, suy ra \(AM \bot BC\). Sử dụng tiên đề Ơ-clit chứng minh ba điểm A, M, H thẳng hàng.
d) Chứng minh tam giác ACF cân tại F và có một góc bằng 600. Sử dụng công thức tính diện tích tam giác bằng nửa tích chiều cao và cạnh tương ứng.

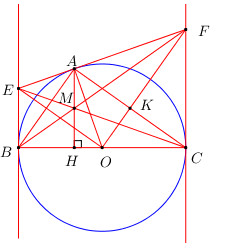
a) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có : \(EA = EB,\,\,FA = FC\)
\( \Rightarrow EF = EA + FA = EB + FC\).
b) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có:
\(OE\) là phân giác của \(\angle AOB\)
\(OF\) là phân giác của \(\angle AOC\).
Mà \(\angle AOB\)và \(\angle AOC\) là 2 góc kề bù
\( \Rightarrow OE \bot OF \Rightarrow \Delta OEF\) vuông tại O.
Áp dụng hệ thức lượng trong tam giác vuông \(OEF\) ta có : \(O{A^2} = EA.FA \Rightarrow {R^2} = BE.CF\).
Advertisements (Quảng cáo)
c) Ta có : \(\dfrac{{FA}}{{EA}} = \dfrac{{FC}}{{EB}} = \dfrac{{FM}}{{BM}} \Rightarrow AM//BE\) (định lí Ta-lét đảo)
Mà \(BE \bot BC\,\,\left( {gt} \right) \Rightarrow AM \bot BC\)
Lại có \(AH \bot BC\,\,\left( {gt} \right) \Rightarrow A,M,H\) thẳng hàng (Tiên đề Ơ-clit).
d) Ta có \(OA = OB = AB = R \Rightarrow \Delta OAB\) đều \( \Rightarrow \angle OBA = {60^0}\).
Ta có : \(\left\{ \begin{array}{l}\angle OBA + \angle ACB = {90^0}\\\angle ACF + \angle ACB = {90^0}\end{array} \right.\)
\(\Rightarrow \angle ACF = \angle OBA = {60^0}\)
Xét tam giác \(ACF\) có :
\(\left\{ \begin{array}{l}FA = FC\,\,\left( {cmt} \right)\\\angle ACF = {60^0}\,\,\left( {cmt} \right)\end{array} \right. \)
\(\Rightarrow \Delta ACF\) đều,
\(A{C^2} = B{C^2} - A{B^2} = {\left( {2R} \right)^2} - {R^2}\)\(\, = 3{R^2}\)
\(\Rightarrow AC = R\sqrt 3 \).
\( \Rightarrow FA = FC = AC = R\sqrt 3 \).
Gọi \(K = AC \cap OF\) ta có :
\(OA = OC = R \Rightarrow O\) thuộc trung trực của \(AC\).
\(FA = FC\,\,\left( {cmt} \right) \Rightarrow F\) thuộc trung trực của \(AC\)
\( \Rightarrow OF\) là trung trực của \(AC \Rightarrow OF \bot AC\) tại \(K\) là trung điểm của \(AC\).
\( \Rightarrow AK = \dfrac{{AC}}{2} = \dfrac{{R\sqrt 3 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(FAK\) có :
\(F{K^2} = F{A^2} - A{K^2} \)\(\,= {\left( {R\sqrt 3 } \right)^2} - {\left( {\dfrac{{R\sqrt 3 }}{2}} \right)^2} = \dfrac{{9{R^2}}}{4}\)
\(\Rightarrow FK = \dfrac{{3R}}{2}\)
Vậy \({S_{\Delta ACF}} = \dfrac{1}{2}FK.AC = \dfrac{1}{2}.\dfrac{{3R}}{2}.R\sqrt 3 \)\(\, = \dfrac{{3{R^2}\sqrt 3 }}{4}\).
Baitapsgk.com
