
Cho đường tròn (O ; R), AB là đường kính. Trên (O) lấy điểm C sao cho AC = R.
a) Tính BC theo R.
b) Tiếp tuyến với đường tròn (O) tại C cắt đườn thẳng AB tại M. Lấy trên (O) điểm D sao cho MD = MC. Chứng minh rằng MD là tiếp tuyến của đường tròn (O).
c) Chứng minh rằng \(M{C^2} = MA.MB\).
d) Kẻ đường kính DE của đường tròn (O), ME cắt (O) tại F. Gọi H là giao điểm của CD với MO. Chứng minh rằng : MF.ME = MH.MO.
a) Áp dụng định lí Pytago trong tam giác vuông.
b) Chứng minh \(\Delta OMC = \Delta OMD\), từ đó suy ra \(\angle ODM = {90^0}\).
c) Chứng minh \(\Delta MAC \sim \pi \Delta MCB\).
d) Chứng minh \(\Delta MDF \sim \Delta MED\) và áp dụng hệ thức lượng trong tam giác vuông.

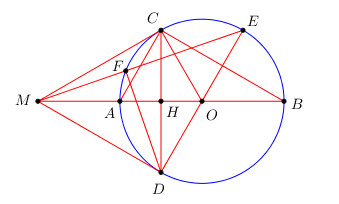
a) Do \(C\) thuộc đường tròn đường kính \(A \Rightarrow \angle ACB = {90^0} \Rightarrow \Delta ABC\) vuông tại \(C\) .
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(B{C^2} = A{B^2} - A{C^2}\)\(\, = {\left( {2R} \right)^2} - {R^2} = 3{R^2}\)
Advertisements (Quảng cáo)
\(\Rightarrow BC = R\sqrt 3 \).
b) Xét \(\Delta OMC\) và \(\Delta OMD\) có :
\(\begin{array}{l}OM\,\,chung\\OC = OD = R\\MC = MD\,\,\left( {gt} \right)\\ \Rightarrow \Delta OMC = \Delta OMD\,\,\left( {c.c.c} \right)\\ \Rightarrow \angle OCM = \angle ODM = {90^0}\end{array}\)
\( \Rightarrow MD \bot OD\) tại \(D\). Mà \(OD\) là bán kính của \(\left( O \right)\).
Vậy \(MD\) là tiếp tuyến của \(\left( O \right)\).
c) Xét \(\Delta OAC\) có \(OA = OC = R\) \( \Rightarrow \Delta OAC\) cân tại \(O \Rightarrow \angle OAC = \angle OCA\).
Mà \(\angle OAC + \angle B = {90^0}\) (hai góc nhọn trong tam giác vuông \(ABC\)).
\(\angle OCA + \angle ACM = \angle OCM = {90^0}\)
\( \Rightarrow \angle ACM = \angle B\).
Xét \(\Delta MAC\) và \(\Delta ACB\) có :
\(\begin{array}{l}\angle BMC\,\,chung;\\\angle ACM = \angle B\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MAC \sim \Delta MCB\,\,\left( {g.g} \right)\\ \Rightarrow \dfrac{{MA}}{{MC}} = \dfrac{{MC}}{{MB}}\\ \Rightarrow M{C^2} = MA.MB\end{array}\)
d) Vì \(F\) thuộc đường tròn đường kính \(DE \Rightarrow \angle DFE = {90^0} \Rightarrow DF \bot EF\)
\(MD\) là tiếp tuyến của \(\left( O \right)\,\,\left( {cmt} \right) \Rightarrow MD \bot DE\).
Xét \(\Delta MDF\) và \(\Delta MED\) có :
\(\begin{array}{l}\angle DME\,\,chung\\\angle DFM = \angle EDM = {90^0}\\ \Rightarrow \Delta MDF \sim \Delta MED\,\,\left( {g.g} \right)\\ \Rightarrow \dfrac{{MD}}{{ME}} = \dfrac{{MF}}{{MD}}\\ \Rightarrow M{D^2} = ME.MF\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông \(ODM\) ta có : \(M{D^2} = MH.MO\).
Vậy \(MH.MO = MF.ME\).
Baitapsgk.com
