
Từ điểm A ngoài đường tròn (O ; R) sao cho OA = 2R vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm).
a) Tính theo R độ dài AB.
b) Đường cao BH của tam giác ABO kéo dài cắt đường tròn (O) tại C. Chứng minh rằng AC là tiếp tuyến của đường tròn (O).
c) Gọi E là giao điểm của OA với đường tròn (O) ( E nằm giữa O và A). Chứng minh rằng E là tâm đường tròn nội tiếp tam giác ABC.
a) Áp dụng định lí Pytago.
b) Chứng minh \(\angle OCA = {90^0} \Rightarrow AC \bot OC\).
c) Chứng minh \(\Delta ABC\) đều và chứng minh \(E\) là trọng tâm tam giác \(ABC\).

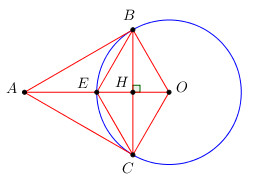
a) Do \(AB\) là tiếp tuyến của \(\left( O \right) \Rightarrow AB \bot OB\) tại \(B \Rightarrow \Delta OAB\) vuông tại \(B\).
Áp dụng định lí Pytago trong tam giác vuông \(OAB\) ta có :
\(O{B^2} = A{B^2} - O{A^2} = {\left( {2R} \right)^2} - {R^2} = 3{R^2}\)
\(\Rightarrow OB = R\sqrt 3 \).
Advertisements (Quảng cáo)
b) Vì \(OA \bot BC\) tại \(H \Rightarrow H\) là trung điểm của \(BC\) (quan hệ vuông góc giữa đường kính và dây cung).
\( \Rightarrow OA\) là trung trực của \(BC\).
\(A \in OA \Rightarrow AB = AC \Rightarrow \Delta ABC\) cân tại \(A \Rightarrow \angle ABC = \angle ACB\).
\(O \in OA \Rightarrow OB = OC \Rightarrow \Delta OBC\) cân tại \(O \Rightarrow \angle OBC = \angle OCB\)
\( \Rightarrow \angle ABC + \angle OBC = \angle ACB + \angle OCB \)
\(\Rightarrow \angle OCA = \angle OBA = {90^0}\)
\( \Rightarrow AC \bot OC\) tại \(C\). Mà \(OC\) là bán kính của \(\left( {O;R} \right)\).
Vậy \(AC\) là tiếp tuyến của \(\left( {O;R} \right)\).
c) Áp dụng hệ thức lượng trong tam giác vuông \(OAB\) ta có :
\(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{R^2}}} + \dfrac{1}{{3{R^2}}} = \dfrac{4}{{3{R^2}}}\)
\(\Rightarrow BH = \dfrac{{R\sqrt 3 }}{2}\)
\( \Rightarrow BC = 2BH = R\sqrt 3 = AB = AC\) \( \Rightarrow \Delta ABC\) đều.
Ta có : \(A{B^2} = AH.OA\) \( \Rightarrow AH = \dfrac{{A{B^2}}}{{OA}} = \dfrac{{3{R^2}}}{{2R}} = \dfrac{{3R}}{2}\).
\(AE = OA - OE = 2R - R = R\) \( \Rightarrow AE = \dfrac{2}{3}AH\), mà \(AH\) là trung tuyến của \(\Delta ABC \Rightarrow E\) là trọng tâm tam giác \(ABC\) .
Lại có \(\Delta ABC\) đều \( \Rightarrow \) Trọng tâm \(E\) đồng thời là tâm đường tròn nội tiếp \(\Delta ABC\).
Baitapsgk.com
