
Cho hàm số \(y = - {x^2}\) .
a) Vẽ đồ thị (P) của hàm số.
b) Tìm trên (P) các điểm có hoành độ \(2, - 2,\sqrt 3 , - \sqrt 3 .\)
c) Tìm trên (P) các điểm có tung độ \( - 3, - \dfrac{3}{2}.\)
b) Muốn tìm tung độ của điểm thuộc parabol có hoành độ \(x = {x_0}\) thay thay \(x = {x_0}\) vào phương trình (P) từ đó ta tìm được y.
c) Muốn tìm hoành độ của điểm thuộc parabol có tung độ \(y = {y_0}\) thay thay \(y = {y_0}\) vào phương trình (P) từ đó ta tìm được x.

a) Bảng giá trị
Bảng giá trị
|
\(x\) |
\( - 2\) |
\( - 1\) |
Advertisements (Quảng cáo) 0 |
1 |
2 |
|
\(y = - {x^2}\) |
\( - 4\) |
-1 |
0 |
-1 |
-4 |
Vậy đồ thị hàm số \(y = {x^2}\) là parabol và đi qua các điểm có tọa độ là \(\left( { - 2; - 4} \right);\left( { - 1; - 1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\)\(\,\left( {2; - 4} \right)\)
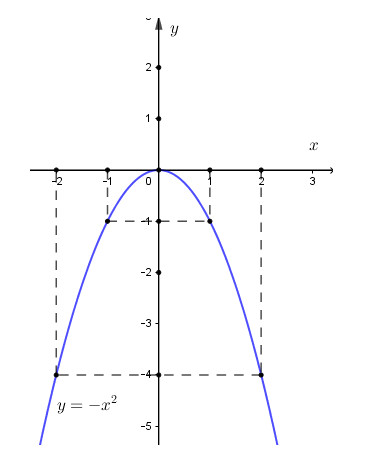
b) Tìm trên (P) các điểm có hoành độ \(2, - 2,\sqrt 3 , - \sqrt 3 .\)
\(\begin{array}{l}y = - {x^2}\\ \Rightarrow y\left( 2 \right) = - {2^2} = - 4 \Rightarrow \,\left( {2; - 4} \right)\\y\left( { - 2} \right) = - {\left( { - 2} \right)^2} = - 4 \Rightarrow \,\left( { - 2; - 4} \right)\\y\left( {\sqrt 3 } \right) = - {\left( {\sqrt 3 } \right)^2} = - 3 \\\Rightarrow \,\left( {\sqrt 3 ; - 3} \right)\\y\left( { - \sqrt 3 } \right) = - {\left( { - \sqrt 3 } \right)^2} = - 3\\ \Rightarrow \,\left( { - \sqrt 3 ; - 3} \right)\end{array}\)
c) Tìm trên (P) các điểm có tung độ \( - 3, - \dfrac{3}{2}.\)
\(\begin{array}{l}y = - {x^2}\\y = - 3 \Rightarrow - {x^2} = - 3 \Leftrightarrow x = \pm \sqrt 3 \\\Rightarrow \,\left( {\sqrt 3 ; - 3} \right);\,\left( { - \sqrt 3 ; - 3} \right)\\y = - \dfrac{3}{2} \Rightarrow - {x^2} = - \dfrac{3}{2} \Leftrightarrow x = \pm \dfrac{{\sqrt 6 }}{2}\\ \Rightarrow \left( {\dfrac{{\sqrt 6 }}{2}; - \dfrac{3}{2}} \right);\left( { - \dfrac{{\sqrt 6 }}{2}; - \dfrac{3}{2}} \right)\end{array}\)
