Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng. Bài 32 trang 116 sgk Toán 9 - tập 1 - Bài 6. Tính chất của hai tiếp tuyến cắt nhau
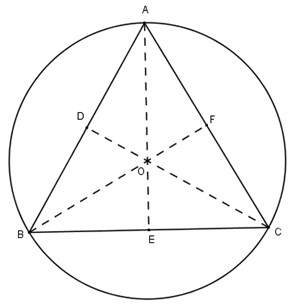
Cho tam giác đều ABC ngoại tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng:
(A) \(6cm^{2}\);
(B) \(\sqrt{3}cm^{2}\);
(C) \(\frac{3\sqrt{3}}{4}cm^{2}\)
(D) \(3\sqrt{3}cm^{2}.\)
Hãy chọn câu trả lời đúng.
Advertisements (Quảng cáo)
Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao \(h=AE=3.OE=3cm.\)
Trong tam giác đều, \(h=\frac{a\sqrt{3}}{2}\) (a là độ dài mỗi cạnh).
Suy ra \(a=\frac{2\cdot h}{\sqrt{3}}=\frac{2\cdot 3}{\sqrt{3}}=2\sqrt{3}(cm).\)
Do đó diện tích tam giác ABC là
\(S=\frac{1}{2}ah=\frac{1}{2}\cdot 2\sqrt{3}\cdot 3=3\sqrt{3}(cm^{2}).\)
Ta chọn (D).