5. Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:
a) \( \left\{ \matrix{2{\rm{x}} - y = 1 \hfill \cr x - 2y = - 1 \hfill \cr} \right. \)
b) \( \left\{ \matrix{2{\rm{x + }}y = 4 \hfill \cr - x + y = 1 \hfill \cr} \right. \)

a) \(\left\{ \matrix{2{\rm{x}} - y = 1 \hfill \cr x - 2y = - 1 \hfill \cr} \right.\)
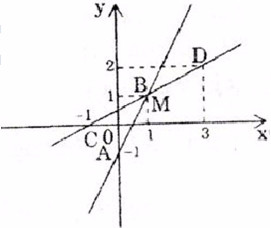
Vẽ (d1): \(2x - y = 1\)
Cho \(x = 0 \Rightarrow y = -1\), ta được \(A(0; -1)\).
Cho \(y = 1 \Rightarrow x = 1\), ta được \(B(1; 1)\).
Vẽ (d2): \(x - 2y = -1\)
Cho \(x = -1 \Rightarrow y = 0\), ta được \(C (-1; 0)\).
Cho \(y = 2 \Rightarrow x = 3\), ta được \(D = (3; 2)\).
Hai đường thẳng cắt nhau tại điểm M có tọa độ \(M( 1, 1)\).
Thay \(x = 1, y = 1\) vào các phương trình của hệ ta được:
Advertisements (Quảng cáo)
\(2 . 1 - 1 = 1\) (thỏa mãn)
\(1 - 2 . 1 = -1\) (thỏa mãn)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 1)\).
b) \(\left\{ \matrix{2{\rm{x + }}y = 4 \hfill \cr - x + y = 1 \hfill \cr} \right.\)
Vẽ (d1): \(2x + y = 4\)
Cho \(x = 0 \Rightarrow y = 4\), ta được \(A(0; 4)\).
Cho \(y = 0 \Rightarrow x = 2\), ta được \(B(2; 0)\).
Vẽ (d2): \(-x + y = 1\)
Cho \(x = 0 \Rightarrow y = 1\), ta được \(C(0; 1)\).
Cho \(y = 0 \Rightarrow x = -1\), ta được \(D(-1; 0)\).
Hai đường thẳng cắt nhau tại điểm N có tọa độ \(N(1;2)\).
Thay \(x = 1, y = 2\) vào các phương trình của hệ ta được:
\(2 . 1 + 2 = 4\) và \(-1 + 2 = 1\) (thỏa mãn)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 2)\).
