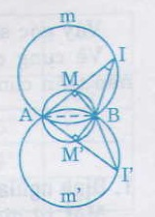
Bài 50. Cho đường tròn đường kính \(AB\) cố định. \(M\) là một điểm chạy trên đường tròn. Trên tia đối của tia \(MA\) lấy điểm \(I\) sao cho \(MI = 2MB\).
a) Chứng minh \(\widehat{AIB}\) không đổi.
b) Tìm tập hợp các điểm \(I\) nói trên.
Hướng dẫn giải:
a) Vì \(\widehat{BMA}\) = \(90^0\) (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông \(MIB\) có \(tg\widehat{AIB}\) = \(\frac{MB}{MI}\) = \(\frac{1}{2}\) =>\(\widehat{AIB}\) = \(26^0 34’\)
Vậy \(\widehat{AIB}\) không đổi.
b) Phần thuận:
Advertisements (Quảng cáo)
Khi điểm \(M\) chuyển động trên đường tròn đường kính \(AB\) thì điểm \(I\) cũng chuyển động, nhưng luôn nhìn đoạn thẳng \(AB\) cố định dưới góc \(26^0 34’\) , vậy điểm \(I\) thuộc hai cung chứa góc \(26^0 34’\) dựng trên đoạn thẳng \(AB\) (hai cung \(\overparen{AmB}\) và \(\overparen{Am’B}\))
Phần đảo:
Lấy điểm \(I’\) bất kì thuộc \(\overparen{AmB}\)
hoặc \(\overparen{Am’B}\), \(I’A\) cắt đường tròn đường kính \(AB\) tại \(M’\).
Tam giác vuông \(BMT\), có \(tg\widehat{I’}\) = \(\frac{M’B}{M’I’}\) = \(tg26^034’\)
Kết luận: Quỹ tích điểm \(I\) là hai cung \(\overparen{AmB}\) và \(\overparen{Am’B}\)