Bài 66. Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm2.
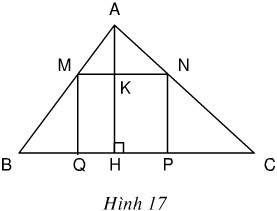

Gọi \(x\) (cm) là độ dài của đoạn \(AK\). Điều kiện \(0 < x < 12\)
Vì \(∆ABC\) đồng dạng \(∆AMN\) nên
\(\eqalign{
& {{MN} \over {BC}} = {{AM} \over {AB}} = {{AK} \over {AH}} = {x \over {12}} \cr
& \Rightarrow MN = {{16x} \over {12}} = {{4{\rm{x}}} \over 3} \cr} \)
Ta có: \(MQ = KH = 12 – x\)
Advertisements (Quảng cáo)
Do đó diện tich hình chữ nhật \(MNPQ\) là: \(\left( {12 - x} \right){{4{\rm{x}}} \over 3}\)
Ta có phương trình:
\(\left( {12 - x} \right){{4{\rm{x}}} \over 3} = 36 \Leftrightarrow {x^2} - 12{\rm{x}} + 27 = 0\)
Giải phương trình ta được:
\({x_1} = 9\) (nhận) hoặc \({x_2} = 3\) (nhận)
Vậy độ dài của đoạn \(AK = 3cm\) hoặc \(9cm\). Khi đó \(M\) sẽ có hai vị trí trên \(AB\) nhưng diện tích hình chữ nhật \(MNPQ\) luôn bằng \(36\) cm2
