Bài 68. Cho ba điểm A, B, C. Bài 68 trang 95 sgk Toán lớp 9 tập 2 - Bài 9. Độ dài đường tròn cung tròn
Bài 68. Cho ba điểm \(A, B, C\) thẳng hàng sao cho \(B\) nằm giữa \(A\) và \(C\). Chứng minh rằng độ dài của nửa đường tròn đường kính \(AC\) bằng tổng các độ dài của hai nửa đường tròn đường kính \(AB\) và \(BC\).
Hướng dẫn giải:
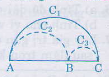
Gọi \({C_1},{C_2},{C_3}\) lần lượt là độ dài của các nửa đường tròn đường kính \(AC, AB, BC\), ta có:
\({C_1}\) = \(π. AC\) (1)
Advertisements (Quảng cáo)
\({C_2}\) = \(π.AB\) (2)
\({C_3}\) = \(π.BC \) (3)
So sánh (1), (2), (3) ta thấy:
\({C_2} + {C_3} = \pi (AB + BC) = \pi AC\)
Vậy \({C_1} = {C_2} + {C_3}\).