Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.. Lý thuyết về một số hệ thức về cạnh và góc trong tam giác vuông - Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
Lý thuyết về một số hệ thức về cạnh và góc trong tam giác vuông
1. Các hệ thức:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Advertisements (Quảng cáo)
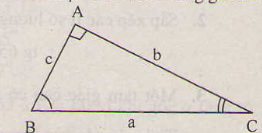
\(b=\)\(a\cdot sinB\)\(=a\cdot cosC\);
\(b=c\cdot tgB=c\cdot cotgC\);
\(c=a\cdot sinC=a\cdot cosB\);
\(c=b\cdot tgC=b\cdot cotgB\).
2. Tam giác vuông:
Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.
