Câu hỏi/bài tập:

Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \(\widehat {BOC} = {120^o}\) và \(\widehat {OCA} = {20^o}\). Tính số đo các góc của tam giác ABC.

+ Ta có \(\widehat A = \frac{{\widehat {BOC}}}{2}\) (góc nội tiếp và góc ở tâm cùng chắn cung nhỏ BC).
+ Tam giác AOC cân tại O nên \(\widehat {AOC} = {180^o} - \widehat {CAO} - \widehat {OCA} = 2.\widehat {OCA}\)
+ \(\widehat B = \frac{{\widehat {AOC}}}{2}\)
Advertisements (Quảng cáo)
+ Do tổng các góc trong tam giác ABC bằng \({180^o}\) nên tính được góc C.

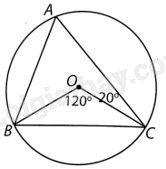
Ta có \(\widehat A = \frac{{\widehat {BOC}}}{2} = {60^o}\) (góc nội tiếp và góc ở tâm cùng chắn cung nhỏ BC).
Tam giác AOC cân tại O nên \(\widehat {AOC} = {180^o} - \widehat {CAO} - \widehat {OCA}\) \( = {180^o} - 2.\widehat {OCA} = {140^o}\).
Suy ra \(\widehat B = \frac{{\widehat {AOC}}}{2} = {70^o}\).
Do tổng các góc trong tam giác ABC bằng \({180^o}\) nên \(\widehat C = {180^o} - \widehat {BAC} - \widehat {ABC} = {50^o}\).
