
Cho đường tròn (O; 5cm) và AB là một dây bất kì của đường tròn đó. Biết \(AB = 6cm\).
a) Tính khoảng cách từ O đến đường thẳng AB.
b) Tính \(\tan \alpha \) nếu góc ở tâm chắn cung AB bằng \(2\alpha \).

a) + Gọi C là trung điểm của AB. Chứng minh CO là đường cao của tam giác OAB nên OC là khoảng cách từ O đến AB.
+ Áp dụng định lý Pythagore vào tam giác AOC vuông tại C tính được OC.
b) + Trong tam giác cân OAB, đường trung tuyến OC cũng là đường phân giác, suy ra \(\widehat {AOC} = \alpha \).
+ Xét tam giác AOC vuông tại C, ta có: \(\tan \alpha = \tan \widehat {AOC} = \frac{{CA}}{{CO}}\).

Advertisements (Quảng cáo)
(H.5.10)
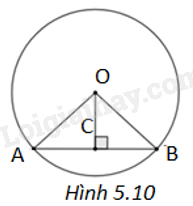
Theo giả thiết, ta có \(OA = OB = 5cm\); \(AB = 6cm\).
a) Gọi C là trung điểm của AB, ta có \(AC = CB = 3cm\). Trong tam giác AOB cân tại O \(\left( {OA = OB} \right)\) có OC là đường trung tuyến nên cũng là đường cao nghĩa là \(CO \bot AB\) tại C.
Vậy OC là khoảng cách từ O đến AB.
Trong tam giác vuông AOC, ta có: \(O{C^2} = O{A^2} - C{A^2} = {5^2} - {3^2} = 16\), suy ra \(OC = 4cm\).
Vậy khoảng cách từ O đến đường thẳng AB bằng 4cm.
b) Trong tam giác cân OAB, đường trung tuyến OC cũng là đường phân giác. Mà \(\widehat {AOB} = 2\alpha \) nên \(\widehat {AOC} = \alpha \).
Xét tam giác AOC vuông tại C, ta có: \(\tan \alpha = \tan \widehat {AOC} = \frac{{CA}}{{CO}} = \frac{3}{4}\).
