
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O’) tại F (E và F khác A). Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.49).
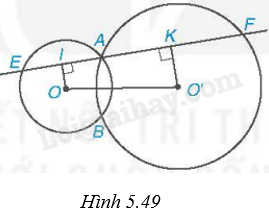
a) Chứng minh rằng tứ giác OO’KI là một hình thang vuông.
b) Chứng minh rằng \(IK = \frac{1}{2}EF\).
c) Khi d ở vị trí nào (d vẫn qua A) thì OO’KI là một hình chữ nhật?

a) Chứng minh \(OI \bot d\), \(KO’ \bot d\) suy ra OI//KO’. Từ đó chứng minh được tứ giác OO’KI là một hình thang vuông.
b) Ta có: \(AE = 2AI\), \(AF = 2AK\) nên \(EF = AE + AF = 2\left( {AI + AK} \right) = 2IK\) nên \(IK = \frac{1}{2}EF\).
c) + Hình thang OO’KI là hình chữ nhật khi IK//OO’.

Advertisements (Quảng cáo)
(H.5.50)
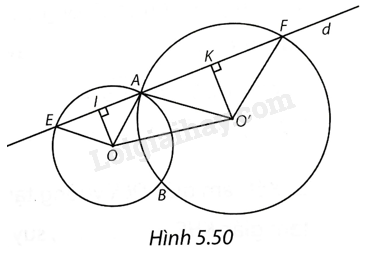
a) \(\Delta \)AOE là tam giác cân tại O (OA=OE) có OI là đường trung tuyến (vì I là trung điểm của AE) nên OI cũng là đường cao, tức là \(\widehat {AIO} = {90^o}\) hay \(OI \bot d\). Tương tự, đối với tam giác AO’F, ta có \(\widehat {AKO’} = {90^o}\) hay \(KO’ \bot d\). Do đó, OI//KO’ (cùng vuông góc với d).
Tứ giác OO’KI có: OI//KO’, \(\widehat {O’KI} = {90^o}\) nên là hình thang vuông.
b) Theo đề bài, \(EI = IA\) và \(AK = KF\) nên ta có \(AE = 2AI\) và \(AF = 2AK\).
Ta có: \(EF = AE + AF = 2AI + 2AK = 2\left( {AI + AK} \right) = 2IK\). Do đó, \(IK = \frac{1}{2}EF\).
c) Khi d đi qua A thì tứ giác OO’KI luôn là hình thang vuông.
Nếu hình thang vuông đó là hình chữ nhật thì IK//OO’, hay d//OO’.
Ngược lại, nếu d//OO’ thì IK//OO’ nên OO’KI là hình chữ nhật.
Vậy để tứ giác OO’KI là hình chữ nhật thì d//OO’.
