
Cho AB là một dây bất kì (không phải là đường kính) của đường tròn (O; 4cm). Gọi C và D lần lượt là các điểm đối xứng với A và B qua tâm O.
a) Hai điểm C và D có nằm trên đường tròn (O) không? Vì sao?
b) Biết rằng ABCD là một hình vuông. Tính độ dài cung lớn AB và diện tích hình quạt tròn tạo bởi hai bán kính OA và OB.

a) Chứng minh \(OA = OC = R\), \(OB = OD = R\) nên hai điểm C và D nằm trên đường tròn (O).
b) + Tính số đo cung nhỏ AB và cung lớn AB.
+ Độ dài cung lớn AB là \(l = \frac{{270}}{{180}}.\pi .4\).
+ Diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB là \(S = \frac{{90}}{{360}}.\pi {.4^2}\)
Advertisements (Quảng cáo)

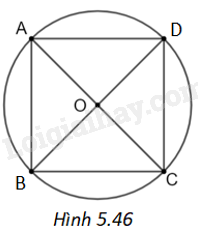
a) Cách 1. Gọi bán kính của đường tròn là R. Do C và D là các điểm đối xứng với A và D qua O nên \(OA = OC = R\) và \(OB = OD = R\).
Do đó, hai điểm C và D nằm trên đường tròn (O).
Cách 2. Do đường tròn là hình có tâm đối xứng là O nên khi \(A \in \left( O \right)\) và \(B \in \left( O \right)\) thì hai điểm đối xứng với A và B qua O cùng nằm trên (O).
b) (H.5.46) Vì ABCD là hình vuông nên \(AC \bot BD\) hay \(\widehat {AOB} = {90^o}\). Suy ra số đo của cung nhỏ AB là 90 độ.
Số đo của cung lớn AB (cũng là cung ACB) là: .
Độ dài cung lớn AB là \(l = \frac{{270}}{{180}}.\pi .4 = 6\pi \left( {cm} \right)\).
Diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB là \(S = \frac{{90}}{{360}}.\pi {.4^2} = 4\pi \left( {c{m^2}} \right)\).
