
Cho điểm B nằm giữa hai điểm A và C, sao cho \(AB = 2cm\) và \(BC = 1cm\). Vẽ các đường tròn (A; 1,5cm), (B; 3cm) và (C; 2cm). Hãy xác định các cặp đường tròn:
a) Cắt nhau;
b) Không giao nhau;
c) Tiếp xúc với nhau.

Hai đường tròn (O; R) và (O’; r) (với \(R > r\)). Khi đó:
+ Hai đường tròn ở ngoài nhau khi \(OO’ > R + r\).
+ Hai đường tròn tiếp xúc ngoài khi \(OO’ = R + r\).
+ Hai đường tròn cắt nhau khi \(R - r
Advertisements (Quảng cáo)
+ Hai đường tròn tiếp xúc trong khi \(OO’ = R - r\).
+ Đường tròn (O) đựng (O’) khi \(OO’

(H.5.47)
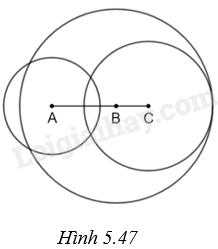
Gọi \({R_A},{R_B}\) và \({R_C}\) lần lượt là bán kính các đường tròn (A), (B), (C). Theo đề bài, ta có \({R_A} = 1,5cm,{R_B} = 3cm,{R_C} = 2cm\), \(AB = 2cm\), \(BC = 1cm\) và \(CA = 3cm\). Ta có:
+) \({R_B} - {R_A} = 1,5
+) \({R_C} - {R_A} = 0,5
+) \(BC = {R_B} - {R_C}\). Do đó, (B) và (C) tiếp xúc trong.
Không có cặp đường tròn nào không giao nhau.
