
Cho tam giác ABC vuông tại A có \(AB = 3cm,AC = 4cm\). Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.

+ Gọi O là trung điểm của BC.
+ Chứng minh \(OA = OB = OC = \frac{1}{2}CB\) nên A, B, C cùng thuộc đường tròn tâm O, bán kính \(R = \frac{{CB}}{2}\).
+ Áp dụng định lý Pythagore trong tam giác ABC vuông tại A để tính BC, từ đó tính được bán kính R.

Advertisements (Quảng cáo)
(H.5.2)
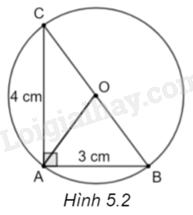
Gọi O là trung điểm của BC. Xét tam giác ABC vuông tại A có AO là đường trung tuyến ứng với cạnh huyền BC nên \(OA = OB = OC = \frac{1}{2}CB\). Do đó, ba điểm A, B, C cùng cách đều O nên A, B, C cùng thuộc đường tròn tâm O, bán kính \(R = \frac{{CB}}{2}\).
Áp dụng định lý Pythagore trong tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2} = 25\) suy ra \(BC = 5cm\).
Do đó, \(R = \frac{{BC}}{2} = \frac{5}{2}\left( {cm} \right)\).
Vậy ba điểm A, B, C cùng thuộc một đường tròn tâm O bán kính \(\frac{5}{2}cm\).
