Câu hỏi/bài tập:

Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm A, B và C, D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng \(\widehat {IBD} = \widehat {ICA},\widehat {IAC} = \widehat {IDB}\) và \(IA.IB = IC.ID\).

+ Do tổng các góc đối của tứ giác ABCD bằng \({180^o}\) nên:
\(\widehat {IBD} = {180^o} - \widehat {ACD} = \widehat {ICA};\widehat {IDB} = {180^o} - \widehat {CAB} = \widehat {IAC}\)
+ Chứng minh $\Delta IBD\backsim \Delta ICA$. Do đó, \(\frac{{IB}}{{IC}} = \frac{{ID}}{{IA}}\), hay \(IA.IB = IC.ID\).
Advertisements (Quảng cáo)

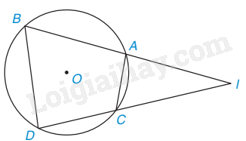
Do tổng các góc đối của tứ giác ABCD bằng \({180^o}\) nên:
\(\widehat {IBD} = {180^o} - \widehat {ACD} = \widehat {ICA}\);
\(\widehat {IDB} = {180^o} - \widehat {CAB} = \widehat {IAC}\)
Mặt khác, từ các đẳng thức trên ta suy ra $\Delta IBD\backsim \Delta ICA$ (g. g).
Do đó, \(\frac{{IB}}{{IC}} = \frac{{ID}}{{IA}}\), hay \(IA.IB = IC.ID\).
