
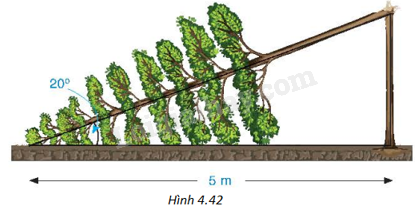
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc \({20^o}\) và chắn ngang lối đi một đoạn 5m (H.4.42). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

+ Gọi A là gốc cây, B là điểm cây gãy, C là ngọn cây.
+ Trong tam giác ABC vuông tại A, ta có: \(AB = AC.\tan C\) tính được AB, \(\cos \widehat {ACB} = \frac{{AC}}{{BC}}\) tính được CB.
+ Chiều cao của cây trước khi đổ gãy là: \(AB + BC\).
Advertisements (Quảng cáo)

(H.4.43)
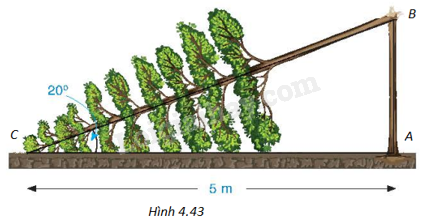
Gọi A là gốc cây, B là điểm cây gãy, C là ngọn cây.
Trong tam giác ABC vuông tại A, ta có \(AB = AC.\tan C = 5.\tan {20^o}\), \(\cos \widehat {ACB} = \frac{{AC}}{{BC}} = \frac{5}{{CB}}\) nên \(BC = \frac{5}{{\cos {{20}^o}}}\).
Do đó, chiều cao của cây trước khi đổ gãy là
\(AB + BC = 5.\tan {20^o} + \frac{5}{{\cos {{20}^o}}} \\= 5\left( {\tan {{20}^o} + \frac{1}{{\cos {{20}^o}}}} \right) \approx 7,1\left( m \right)\)
