Câu hỏi/bài tập:

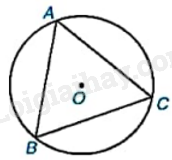
Cho tam giác đều ABC nội tiếp đường tròn (O) như hình bên. Phép quay ngược chiều \({60^o}\) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.

+ Theo hình vẽ ta thấy \(ADBECF\) là lục giác lồi và nội tiếp đường tròn \(\left( {O,R} \right).\)
+ Chứng minh tam giác \(AOD,DOB\) là các tam giác đều. Suy ra \(AD = DB = OD = R.\)
+ Chứng minh tương tự có \(AD = DB = BE = EC = CF = FA = R.\)
+ Chứng minh $\text{sđ}\overset\frown{AOD}=\text{sđ}\overset\frown{DOB}=\text{sđ}\overset\frown{BOE}=\text{sđ}\overset\frown{EOC}=\text{sđ}\overset\frown{COF}=\text{sđ}\overset\frown{FOA}={{60}^{\text{o}}}.$ Từ đó tính được các góc của lục giác đều \(ADBECF\).
+ Lục giác có tất cả các góc bằng nhau, tất cả các cạnh bằng nhau nên là lục giác đều.
Advertisements (Quảng cáo)

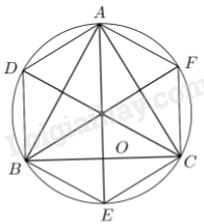
Theo hình vẽ, ta thấy \(ADBECF\) là lục giác lồi và nội tiếp đường tròn \(\left( {O,R} \right).\)
Ta có \(\widehat {AOD} = {60^{\rm{o}}},\,\widehat {DOB} = \widehat {AOB} - \widehat {AOD} = 2\widehat {ACB} - \widehat {AOD} = {60^{\rm{o}}}.\) Do đó các tam giác cân \(AOD,DOB\) là các tam giác đều. Suy ra \(AD = DB = OD = R.\)
Tương tự, ta suy ra: \(AD = DB = BE = EC = CF = FA = R.\)
Như vậy ta được lục giác lồi \(ADBECF\) có các cạnh bằng nhau và nội tiếp đường tròn \((O).\)
Mặt khác, tương tự như trên ta có $\text{sđ}\overset\frown{AOD}=\text{sđ}\overset\frown{DOB}=\text{sđ}\overset\frown{BOE}=\text{sđ}\overset\frown{EOC}=\text{sđ}\overset\frown{COF}=\text{sđ}\overset\frown{FOA}={{60}^{\text{o}}}.$
Do đó các góc của lục giác này là các góc nội tiếp của \((O)\) chắn cung có số đo bằng \(\frac{4}{6} \cdot {360^{\rm{o}}}.\)
Vậy các góc của lục giác \(ADBECF\) bằng nhau và bằng \(\frac{4}{{12}} \cdot {360^{\rm{o}}} = {120^{\rm{o}}}.\) Vậy \(ADBECF\) là lục giác đều.
