Câu hỏi/bài tập:

Cho ngũ giác đều ABCDE có các cạnh bằng 4cm nội tiếp một đường tròn (O).
a) Tính bán kính của (O) biết rằng ta lấy \(\cos {54^o} \approx 0,59\).
b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.

a) + Nhận thấy $\overset\frown{AB}=\overset\frown{BC}=\overset\frown{CD}=\overset\frown{DE}=\overset\frown{EA}$, từ đó tính được góc AOB.
+ Gọi M là trung điểm của AB. Chứng minh OM vuông góc với AB và OM là tia phân giác của góc AOB, từ đó tính được góc AOM và góc MAO.
+ Bán kính của (O) là \(R = \frac{{AM}}{{\cos \widehat {MAO}}}\).
Advertisements (Quảng cáo)
b) Phép quay ngược chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).

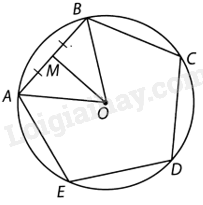
a) Ta thấy các cung nhỏ sau thỏa mãn: $\overset\frown{AB}=\overset\frown{BC}=\overset\frown{CD}=\overset\frown{DE}=\overset\frown{EA}$. Suy ra $\widehat{AOB}=sđ\overset\frown{AB}=\frac{{{360}^{o}}}{5}={{72}^{o}}$.
Gọi M là trung điểm của AB. Vì tam giác AOB cân tại O nên OM vuông góc với AB và OM là tia phân giác của góc AOB. Suy ra: \(\widehat {AOM} = \frac{{\widehat {AOB}}}{2} = \frac{{{{72}^o}}}{2} = {36^o}\).
Như vậy \(\widehat {MAO} = {90^o} - \widehat {AOM} = {54^o}\)
Bán kính của (O) là: \(R = \frac{{AM}}{{\cos \widehat {MAO}}} = \frac{{AM}}{{\cos {{54}^o}}} \approx \frac{2}{{0,59}} \approx 3,39\left( {cm} \right)\).
b) Năm phép quay ngược chiều giữ nguyên ngũ giác đều là các phép quay ngược chiều lần lượt \({72^{\rm{o}}},\,\,{144^{\rm{o}}},\) \({216^{\rm{o}}},\,\,{288^{\rm{o}}},\,\,{360^{\rm{o}}}\) với tâm O.
